M2 - Bases de dades / UF1NF2: Conceptes del model entitat-relació

Les estructures bàsiques del model Entitat-Relació (model ER) es corresponen, fonamentalment, amb els conceptes proposats en la formulació original d’aquest model que va fer el Dr. Peter Pin Shan Chen en el seu treball The Entity-Relationship Model.

La notació d’aquestes construccions és fonamentalment diagramàtica. Es coneixen com a diagrames ER o diagrames Chen.

Els diagrames ER són molt eficaços a l’hora de modelitzar la realitat per obtenir un esquema conceptual entenedor.

Entitats i atributs

Una entitat és alguna cosa que existeix en el món real, distingible de la resta de coses, i de la qual ens interessen algunes propietats.

Les entitats poden tenir una existència física, com per exemple una persona, un cotxe o un llibre, però també poden consistir en conceptes més abstractes, com ara una assegurança o un deute.

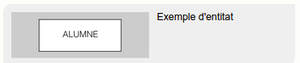
Exemple d'entitat

Imaginem que estem dissenyant la BD d’un institut de secundària, dedicat a l’ensenyament de diferents cicles formatius de formació professional. Cada persona concreta, alumne de l’institut esmentat, existeix en el món real i, per tant, es pot considerar una entitat.

Les entitats en els diagrames ER es representen amb un rectangle.

Amb el terme entitat es pot fer referència a un objecte específic del món real, però també a un conjunt d’objectes semblants, dels quals ens interessen les mateixes característiques. Per tant, hem de distingir:

• Entitats-instància, com a objectes concrets del món real (per exemple, l’alumne Manel Riba és una entitat-instància).
• Entitats-tipus, com a conjunts d’entitats-instància (per exemple, l’entitat tipus alumne).

Anomenem atributs les característiques que ens interessen de les entitats.

Habitualment, només ens interessarà modelitzar una part dels atributs d’una entitat, ja que hi podrà haver dades que només seran d’utilitat en àmbits molt específics.

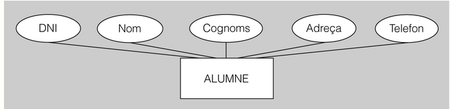
Exemples d'atributs

En una entitat-instància referent als alumnes d’un institut, ens pot resultar interessant recollir certes dades personals, per tal d’identificar correctament els alumnes a l’hora de comunicar-nos amb ells, o d’expedir notes i títols acadèmics, com ara el DNI, el nom, els cognoms, l’adreça, el telèfon, etc.

En canvi, altres dades de la mateixa entitat no seran d’interès per a nosaltres, encara que sí que ho puguin ser per a una BD que pertanyi a un altre àmbit. Per exemple, des d’un punt de vista sanitari, podria ser interessant registrar l’alçada, el pes o el grup sanguini d’aquestes mateixes persones.

Els atributs en els diagrames ER es representen amb una el·lipse.

Domini dels atributs

Conjunt de valors acceptables per a l'atribut en qüestió.

Exemples de domini i de valors vàlids

El domini de l’atribut Nom de l’entitat ALUMNE podria consistir en el conjunt de totes les cadenes de caràcters possibles d’una longitud determinada, tot excloent les xifres i els caràcters especials. Serien valors vàlids per a l’atribut Nom, definit d’aquesta manera, “Laia”, “Pol”, etc. En canvi, no ho serien, per exemple, una data, un nombre o una cadena de caràcters que n’inclogués algun d’especial, com ara “Mariona”.

Valor nul dels atributs

Els atributs d’una entitat-instància poden no tenir cap valor per a algun atribut concret. En aquests casos, també es diu que l’atribut té valor nul.

Exemple de valor nul

Pot passar que un alumne no tingui telèfon. Aleshores, l’atribut Telefon de l’entitat ALUMNE no contindrà cap valor o, dit d’una altra manera, tindrà un valor nul.

Atributs simples i compostos

Un atribut simple no es pot dividir en parts més petites sense que això comporti la pèrdua del seu significat.

Exemple d'atribut simple

L’atribut Nom és un atribut simple, perquè el seu significat és indivisible (encara que en alguns casos emmagatzemi noms compostos, com ara Joan Manel), i per tant no té sentit dividir el seu valor en cadenes de caràcters més petites per tractar-les per separat.

Un atribut compost és el que està subdividit en parts més petites (que també tenen la consideració d’atributs), les quals tenen un significat propi.

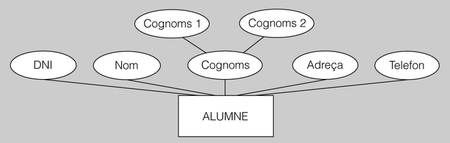
Exemple d'atribut compost

L’atribut Cognoms es pot tractar com un atribut compost, perquè es pot dividir en dues parts més petites (dos atributs, en definitiva) que emmagatzemin, una, el primer cognom, i l’altra el segon cognom. Aquests dos atributs es poden tractar per separat sense problemes.

Com que moltes persones estrangeres només tenen un cognom, en aquest exemple, l’atribut Cognom1 sempre tindrà algun valor per a qualsevol entitat-instància, però l’atribut Cognom2 haurà d’admetre valors nuls.

Pot resultar interessant utilitzar atributs compostos si ens consta que els usuaris es referiran, de vegades, a l’atribut globalment considerat, i de vegades als seus components per separat.

D’altra banda, els atributs compostos agrupen els atributs relacionats, estructurant-los jeràrquicament, de manera que normalment contribueixen a la comprensibilitat dels models.

Atributs monovaluats i multivaluats

Un atribut monovaluat és el que només pot emmagatzemar, com a màxim, un sol valor per a cada entitat instància concreta, en un moment determinat.

Exemple d'atribut monovaluat

És evident que cada persona només pot tenir un DNI vàlid. Per tant, l’atribut DNI de l’entitat ALUMNE s’haurà de tractar necessàriament com un atribut monovaluat.

Un atribut multivaluat pot emmagatzemar, per a cada entitat instància concreta, diferents valors al mateix temps.

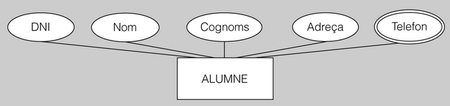
Exemple d'atribut multivaluat

En el món real, una persona pot tenir més d’un telèfon. Per exemple, pot disposar d’un telèfon fix al domicili particular, d’un altre a la feina, i a més pot tenir un telèfon mòbil. Per tant, l’atribut Telefon de l’entitat ALUMNE es pot tractar com un atribut multivaluat.

Els atributs multivaluats es representen en els diagrames ER amb una el·lipse de doble traç.

Cardinalitat dels atributs

Si cal, es poden especificar a continuació del nom de l’atribut, entre parèntesis i separats per comes, el límit màxim i el mínim de valors que s’han d’emmagatzemar, això és la cardinalitat dels atributs. I es poden presentar les opcions següents:

• NomAtribut (1, 1): atribut univaluat obligatori (valor per defecte, si no s’especifica res).

• NomAtribut (0, 1): atribut univaluat opcional (admet valors nuls).

• NomAtribut (1, n): atribut multivaluat obligatori (no admet valors nuls).

• NomAtribut (0, n): atribut multivaluat opcional (admet valors nuls).

Exemples de límits superior i inferior

Seguint amb el cas de l’atribut Telefon, es podria establir, per exemple, un límit inferior a 0 (ja que un alumne pot no disposar de cap telèfon durant un període de temps determinat) o a 1 (si volem obligar l’alumne a donar un telèfon de contacte, encara que no sigui el seu, sinó el d’un familiar, amic o veí).

I es podria limitar el nombre màxim de telèfons a emmagatzemar, per exemple, a 2 (si es preveu la possibilitat, força habitual, de tenir un fix i un mòbil) o a 3 (si, a més, considerem la possibilitat de registrar el telèfon del centre de treball).

Atributs derivats

Es diu que un atribut és derivat quan el seu valor es pot calcular a partir d’altres atributs o bé d’altres entitats interrelacionades.

Quan un atribut serveix per calcular el valor d’un atribut derivat, se’l considera atribut base d’aquest.

Exemples d'atribut derivat

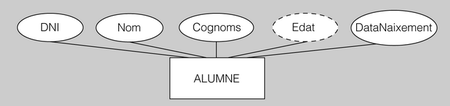
Podríem necessitar saber quina és l’edat en anys dels alumnes, per tal de permetre’ls sortir o no de l’institut durant els períodes d’esbarjo, en funció d’aquella. Si l’entitat ALUMNE té un atribut anomenat DataNaixement, en podríem modelitzar un altre de derivat, anomenat Edat, que es calculés a partir de la data actual (prenent la data del sistema) de la data de naixement (registrada en l’atribut DataNaixement).

També podríem necessitar saber el nombre total d’assignatures a les quals està matriculat cada alumne. Podríem establir un atribut derivat anomenat NombreAssignatures, el valor del qual es calcul és en funció del nombre d’ocurrències d’una altra entitat-tipus anomenada ASSIGNATURA interrelacionades amb cadascuna de les instàncies de l’entitat ALUMNE.

Els atributs derivats constitueixen una redundància, és a dir, una repetició normalment innecessària de dades. Per aquest motiu, les dades dels atributs derivats inclosos en els diagrames ER no s’acostumen a emmagatzemen (i molt especialment si traduïm aquest esquema conceptual a l’esquema lògic més freqüentment utilitzat, és a dir, al model relacional), sinó que es calculen quan és necessari.

Clau primària

L’atribut o el conjunt d’atributs que identifiquen unívocament les entitats instància s’anomenen clau primària de l’entitat.

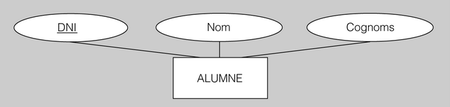
La clau primària en els diagrames ER es representa subratllant els atributs que la formen.

Exemples de clau primària

Podríem seleccionar l’atribut DNI de l’entitat ALUMNE com a clau primària, ja que sabem que en el món real no han d’existir dos documents d’identitat iguals i, per tant, ens servirà amb tota seguretat per distingir qualsevol alumne de la resta.

En els països on no existeixen documents d’identitat, com els anglosaxons, hauríem d’optar per una solució alternativa. Podríem afegir al nostre model un atribut identificador, de tipus codi, encara que aquest no existís al món real: CodiAlumne.

O també podríem considerar com a clau primària un conjunt d’atributs tal que fes impossible o, si més no, molt difícil, que es repetissin les combinacions dels seus valors per a diferents entitats-instància: Nom+Cognoms+Telefon.

Notació

Notacions ER alternatives

Actualment no existeix cap notació estandarditzada universalment per representar els esquemes del model ER. Cada recurs bibliogràfic o cada programari de disseny presenta, doncs, variacions i ampliacions sobre la reduïda notació proposada originàriament per Peter Chen.

El model ER ens permet representar entitats i atributs mitjançant una senzilla notació diagramàtica.

En aquesta representació respectarem les característiques següents:

• Com a regla general, no farem servir accents ni caràcters especials, només lletres i xifres.

• Representarem les entitats tipus escrivint el seu nom en majúscules i en singular, a dins d’un rectangle.

• Representarem cada atribut escrivint el seu nom amb la primera lletra en majúscula i la resta en minúscules, dins d’una el·lipse unida amb un guió amb el rectangle que representa l’entitat tipus de la qual formen part:

• Si un atribut té un nom compost, cada nom començarà amb majúscula per tal de fer-lo més llegidor. Per exemple, TelefonFix, TelefonMobil.

• Si el nom d’un atribut correspon a unes sigles, ha d’anar íntegrament en majúscules, com ara DNI (document nacional d’identitat).

• Les el·lipses dels atributs en què es pot descompondre un atribut han d’anar unides amb un guió amb l’el·lipse de l’atribut compost.

• L’el·lipse d’un atribut multivaluat estarà formada per un traç doble.

• Els límits d’un atribut multivaluat, en cas d’existir, s’han d’especificar a continuació del nom de l’atribut, entre parèntesis i separats per una coma.

• L’el·lipse d’un atribut derivat estarà formada per un traç puntejat.

• Els atributs que formen part d’una clau primària han d’anar subratllats.

Si hem d’establir qualsevol altra característica de les dades que no tingui predefinida una notació diagramàtica concreta, haurem d’afegir al diagrama les especificacions textuals necessàries.

Interrelacions

Una interrelació consisteix en una associació entre dues o més entitats (referència tant a una associació entre diferents entitats instància, como entre diferents entitats tipus).

Exemple d'interrelació

Ja coneixem l’entitat ALUMNE. Però per dissenyar la BD del nostre institut necessitarem més entitats. Per exemple, serà convenient disposar d’una entitat per emmagatzemar les assignatures que conformin l’oferta formativa del centre. Podem anomenar, aquesta nova entitat, ASSIGNATURA.

En un centre educatiu, els alumnes es matriculen d’assignatures. Doncs bé, per modelitzar aquesta característica del món real, no necessitarem cap nova entitat. Només ens caldrà establir una associació entre les dues entitats de què disposem, ALUMNE i ASSIGNATURA, mitjançant una interrelació.

D’aquesta manera, modelitzarem l’associació de cada alumne amb totes les assignatures en què estigui matriculat, i, recíprocament, de cada assignatura amb tots els estudiants respectius. Podríem anomenar aquesta interrelació, per exemple, Matricula.

Les interrelacions en els diagrames ER es representen amb un rombe.

Atributs de les interrelacions

De vegades, ens pot interessar reflectir algunes característiques de determinades interrelacions. La manera de fer-ho és afegir els atributs necessaris, com faríem si treballéssim amb entitats. Aquests atributs són els atributs de la interrelació.

Exemple d'atribut d'interrelació

La secretaria del nostre institut necessitarà tenir constància, com a mínim, de la nota final obtinguda per cada alumne en cada assignatura en què s’hagi matriculat alguna vegada.

La manera més senzilla de fer-ho seria afegir, a la interrelació Matricula, un atribut anomenat, per exemple, NotaFinal, que servís per emmagatzemar aquesta dada per a cada associació existent entre instàncies de les entitats ALUMNE i ASSIGNATURA.

Les propietats dels atributs de les interrelacions són idèntiques a les descrites prèviament en relació als atributs de les entitats.

Grau de les interrelacions

El grau d’una interrelació depèn del nombre d’entitats que aquesta associa.

la figura del subapartat anterior “Atributs de les interrelacions” mostra un exemple d’interrelació de grau dos (només associa dues entitats: ALUMNE i ASSIGNATURA).

Les interrelacions de grau dos també s’anomenen binàries. I les de grau superior a dos s’anomenen genèricament n-àries. Les interrelacions n-àries de grau tres també poden ser anomenades ternàries, i les de grau quatre, quaternàries.

Exemple d'interrelació de grau tres

Fins ara, la interrelació Matricula només permet emmagatzemar una matrícula de cada alumne en cada assignatura, i el seu atribut NotaFinal només permet reflectir una sola nota final de curs.

Però aquest esquema no permet modelitzar el fet que un alumne es pot haver de matricular més d’un cop d’una mateixa assignatura (i obtenir una nota final en cada nova matrícula) fins a obtenir una qualificació igual o superior a l’aprovat.

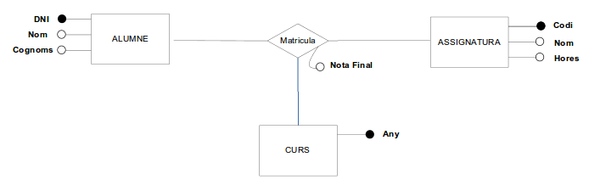
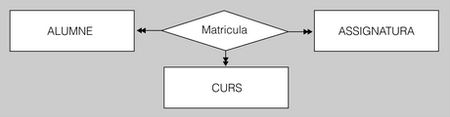
Una manera d’aconseguir representar aquesta característica del món real consistiria a afegir, en nostre disseny, una nova entitat que fes referència a l’element temporal. La podríem anomenar CURS, per exemple.

I, a continuació, només cal que la interrelació Matricula (tot conservant l’atribut NotaFinal) interrelacioni tres entitats: ALUMNE, ASSIGNATURA i CURS.

I el nou esquema ja permetrà registrar matrícules successives d’un mateix alumne en una mateixa assignatura, però al llarg de diferents cursos acadèmics, amb les respectives qualificacions obtingudes.

Connectivitat de les interrelacions

La connectivitat (també anomenada cardinalitat) d’una interrelació indica el tipus de correspondència que hi ha entre les ocurrències de les entitats que ella mateixa permet associar.

Tractant-se d’interrelacions binàries, la cardinalitat expressa el nombre màxim d’instàncies d’una de les entitats amb les quals una instància de l’altra entitat pot estar associada segons la interrelació en qüestió.

Una N en un costat de la interrelació també es representa freqüentment amb un asterisc (*).

Les interrelacions binàries poden oferir tres tipus de connectivitat:

• Un a un (1:1)

• Un a uns quants (1:N)

• Uns quants a uns quants (N:M)

Un 1 al costat d’una entitat indica que, com a màxim, només una de les seves instàncies (la qual podrà variar en cada cas) tindrà la possibilitat d’estar associada amb cadascuna de les instàncies de l’altra entitat.

Si més d’un extrem de la interrelació té una N, per raó d’elegància es representa amb consonants successives, començant per M: M, N, P, Q, etc.

La cardinalitat 1 també es pot representar convertint la línia que uneix la interrelació amb l’entitat en una fletxa que apunti cap a l’entitat.

En canvi, una N (o una M) al costat d’una entitat indica que serà una pluralitat de les seves instàncies (les quals també podran variar en cada cas) la que tindrà la possibilitat d’estar associada amb cadascuna de les instàncies de l’altra entitat.

La cardinalitat N (o M) també es pot representar amb una fletxa de doble punta que vagi de la interrelació cap a l’entitat.

És molt important adonar-se que, independentment del tipus de connectivitat, una interrelació només permet associar una sola vegada unes entitats instància determinades entre elles.

Exemple de connectivitat 1:1

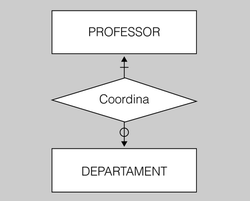
Com els alumnes, els professors també formen part de la comunitat educativa (a més d’altres col·lectius que de moment no necessitem tenir en compte).

Els professors s’organitzen professionalment en departaments, en funció de la seva especialitat (per exemple: matemàtiques, filosofia, informàtica, etc.).

Per tal de reflectir aquestes dues realitats, haurem d’afegir al nostre model dues noves entitats: PROFESSOR i DEPARTAMENT.

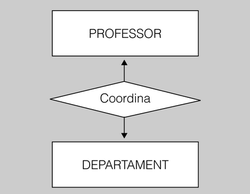
Cada departament és coordinat per un sol professor, i un professor només pot coordinar un sol departament. Per tal de reflectir aquesta circumstància, haurem d’establir una interrelació entre les entitats PROFESSOR i DEPARTAMENT amb cardinalitat 1:1. Podem anomenar la nova interrelació Coordina.

Exemple de connectivitat 1:N

Ja sabem que tot professor d’institut està assignat a un departament. Però encara ens falta establir una nova interrelació entre PROFESSOR i DEPARTAMENT que reflecteixi aquesta realitat. La podem anomenar Treballa.

Com que cada professor només pot treballar a un departament, al costat de la interrelació que connecta l’entitat DEPARTAMENT, hi anirà un 1.

Inversament, com que cada departament pot tenir més d’un professor assignat, al costat de la interrelació que connecta l’entitat PROFESSOR, hi anirà una N.

Exemple de connectivitat N:M

Imaginem que al nostre institut s’organitzen activitats esportives extraescolars. Cal incorporar al nostre model una nova entitat (que podem anomenar ESPORT, per exemple) i una nova interrelació que l’associï amb l’entitat ALUMNE (que podem anomenar Practica).

Els alumnes tenen la possibilitat d’inscriure’s com a practicants d’un o més esports. I els esports, evidentment, poden ser practicats per més d’un alumne. Per tant, a un costat de la interrelació, hi anirà una N, i a l’altre una M.

Dependències d'existència a les interrelacions binàries

De vegades, una entitat instància només té sentit si existeix com a mínim una altra entitat instància associada amb ella mitjançant una interrelació binària determinada. En aquests casos, es diu que la darrera entitat és una entitat obligatòria per a la interrelació. Altrament, es diu que es tracta d’una entitat opcional per a la interrelació.

Les entitats opcionals en els diagrames ER es representen superposant un cercle a la línia que uneix l’entitat a la relació.

Les entitats obligatòries en els diagrames ER es representen superposant un petit guió a la línia que uneix l’entitat a la relació.

Un cercle en la línia de connexió entre una entitat i una interrelació indica que l’entitat és opcional en la interrelació. L’obligatorietat d’una entitat en una interrelació s’indica amb un guionet perpendicular a la línia que uneix l’entitat amb la interrelació. Si no es consigna ni un cercle ni una línia perpendicular, es considera que la dependència d’existència és desconeguda.

Tindrem en compte aquesta característica només pel que faci a les interrelacions binàries, però no a les n-àries.

Exemple de dependències d'existència

L’entitat PROFESSOR és obligatòria en la interrelació Coordina. D’aquesta manera, s’indica que no pot existir un departament que no tingui cap professor que faci de coordinador del departament. L’entitat DEPARTAMENT, en canvi, és opcional en la interrelació Coordina, ja que la majoria dels professors no coordinaran cap departament.

Interrelacions ternàries i n-àries

La cardinalitat de les interrelacions n-àries expressa el nombre màxim d’instàncies d’una de les entitats amb les quals una combinació concreta d’instàncies de les altres entitats pot estar associada segons la interrelació en qüestió.

Les interrelacions ternàries poden oferir quatre tipus de connectivitat:

• 1:1:1

• 1:1:N

• 1:M:N

• M:N:P

Exemple de connectivitat M:N:P

Ja coneixem la interrelació Matricula, que associa les entitats ASSIGNATURA, ALUMNE i CURS. Però encara no hem establert les seves cardinalitats.

Un alumne, en un curs determinat, es pot matricular d’unes quantes assignatures. Per tant, al costat de l’entitat ASSIGNATURA, hi haurà una N (però si només es pogués matricular d’una sola assignatura, hi hauria d’haver un 1).

Un alumne es pot haver de matricular d’una mateixa assignatura durant més d’un curs acadèmic, fins que la superi. Per tant, al costat de l’entitat CURS, hi haurà una N (però si només fos possible matricular-se un cop d’una assignatura, hi hauria d’haver un 1).

I és evident que, durant un curs acadèmic, diferents alumnes poden estar matriculats en una mateixa assignatura. Per tant, al costat de l’entitat ALUMNE, també hi haurà una N (però si només s’acceptés la matrícula d’un alumne per assignatura i curs, hi hauria d’haver un 1).

Límits de cardinalitat

De vegades, pot resultar útil establir límits mínims i màxims a les cardinalitats de les interrelacions. Per fer-ho, només cal afegir una etiqueta del tipus mín..màx, per tal d’expressar els límits respectius, al costat de la línia que uneix cada entitat amb la interrelació.

Els valors mín i màx podran tenir els valors següents:

• Zero, per indicar la possibilitat que no existeixi cap associació entre instàncies.

• Qualssevol nombres enters, per indicar un límit mínim o màxim concret de possibilitats d’associació entre instàncies.

• Un asterisc (*), per indicar la possibilitat d’un nombre il·limitat d’associacions entre instàncies.

Exemple de límits de cardinalitat

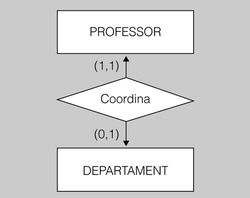
Ja coneixem la interrelació Coordina, que associa les entitats PROFESSOR i DEPARTAMENT amb cardinalitat 1:1.

Cada departament ha de tenir assignat un, i només un, professor que el coordini. Per tal de reflectir aquesta limitació, haurem d’afegir l’etiqueta 1..1 al costat de la línia que uneix l’entitat PROFESSOR amb la interrelació Coordina.

D’altra banda, no tots els professors s’encarreguen de coordinar un departament (de fet, el més freqüent és que no se n’encarreguin). I si ho fan, només es poden encarregar de la coordinació d’un. Per tal de reflectir aquesta limitació haurem d’afegir l’etiqueta 0..1 al costat de la línia que uneix l’entitat DEPARTAMENT amb la interrelació Coordina.

Interrelacions recursives

Una interrelació recursiva associa les instàncies d’una entitat amb altres instàncies de la mateixa entitat.

Es diu que una interrelació recursiva és de grau 2 (o binària) si només hi participa una entitat, la qual es relaciona amb ella mateixa.

Exemple d'interrelació recursiva binària

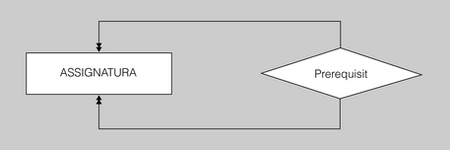
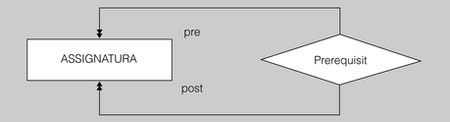
Imaginem que al nostre institut s’estableix, com a requisit per cursar certes assignatures, el fet d’haver superat prèviament una altra o unes altres assignatures.

Podríem modelitzar aquesta situació mitjançant una interrelació recursiva binària sobre l’entitat ASSIGNATURA, i anomenar-la, per exemple, Prerequisit.

Si considerem que cada assignatura pot tenir més d’una altra assignatura com a prerequisit, i que al mateix temps cada assignatura pot ser prerequisit d’una pluralitat d’assignatures, la cardinalitat hauria de ser M:N.

Les interrelacions recursives en els diagrames ER es representen connectant una mateixa entitat més d’una vegada, mitjançant una única relació.

Si en una interrelació recursiva participen, addicionalment, més entitats, parlarem d’interrelacions recursives de grau 3 (o ternàries), de grau 4 (o quaternàries), i així successivament.

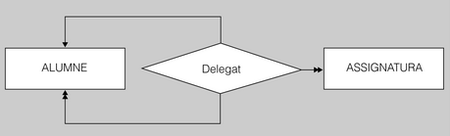
Exemple d'interrelació recursiva ternària

Cada alumne del nostre institut té un delegat per assignatura, que el representa davant del professorat que la imparteix, per tal de fer més fluïdes les comunicacions sobre les qüestions relatives al funcionament d’aquella que no siguin d’índole personal.

Podríem modelitzar aquesta situació mitjançant una interrelació recursiva ternària, anomenada, per exemple, Delegat. Una ocurrència d’aquesta interrelació associarà un alumne que actuarà com a delegat en l’àmbit d’una assignatura, un altre alumne que actuarà com a estudiant de la mateixa assignatura, i l’assignatura en qüestió.

La connectivitat és 1:M:N. En els dos costats de l’entitat ALUMNE hi ha un 1 i una N, perquè, d’una banda, un delegat d’una assignatura pot representar més d’un estudiant (N), i, d’una altra banda, un estudiant d’una assignatura només pot tenir un sol representant en l’àmbit d’aquesta (1). I al costat de l’entitat ASSIGNATURA hi ha una M, perquè un alumne pot actuar com a representant d’un altre en diferents àmbits, corresponents a diferents assignatures.

En una interrelació no recursiva, el paper, o rol, que interpreta cada entitat implicada se sobreentén i, per tant, no cal especificar-lo.

En el cas de les interrelacions recursives, pot tenir importància especificar els diferents papers o rols que interpreten les instàncies d’una mateixa entitat, si aquests rols no coincideixen plenament. Si el rol és exactament el mateix, no cal especificar-lo.

Exemple de diferenciació de rols

Podríem etiquetar les dues línies de la interrelació Prerequisit com a “pre” i “post”, per exemple, per tal de modelitzar en el primer cas el rol de prerequisit acadèmic i, en el segon cas, el rol d’assignatura autoritzada.

Notació

Com amb les entitats, la notació diagramàtica per representar les interrelacions i les seves propietats també és força senzilla:

• Tota interrelació es representa amb un rombe, que va unit, mitjançant línies, a totes les entitats que associa.

• Els atributs d’una interrelació, quan existeixen, es representen de la mateixa manera que els atributs d’una entitat.

• La connectivitat d’una interrelació es representa afegint una etiqueta amb un 1 o una N, segons calgui, a cadascuna de les línies que la uneix amb les entitats que hi participen.

• L’opcionalitat es representa superposant un cercle a la línia de connexió corresponent, i l’obligatorietat, superposant un petit guió perpendicular a la línia de connexió de què es tracti.

• Si cal establir límits (0, enter, *) a la cardinalitat d’una interrelació, s’ha d’afegir a cadascuna de les seves línies de connexió una etiqueta amb el límit inferior i el superior separats per dos punts seguits.

• La recursivitat d’una interrelació es representa fent arribar dues línies de connexió a la mateixa entitat. Si participen més entitats de la mateixa interrelació recursiva, s’hi han de fer arribar les línies de connexió corresponents des de la interrelació.

• Si cal fer una diferenciació dels rols d’una interrelació recursiva, s’ha d’afegir una etiqueta, amb l’especificació textual adequada, al costat de cadascuna de les línies de connexió.

Entitats febles

Les entitats que disposen d’un atribut o, si no, d’un conjunt d’atributs capaços d’establir una clau primària que serveixi per distingir cada instància de l’entitat de la resta d’ocurrències es poden anomenar, més específicament,entitats fortes.

Les entitats febles són aquelles que no disposen de prou atributs per a designar unívocament les seves instàncies. Per tal d’aconseguir-ho, han d’estar associades, mitjançant una interrelació, amb una entitat forta que les ajudi.

La interrelació entre una entitat feble i la seva forta associada és sempre de cardinalitat 1:N, i es resta l’1 al costat de l’entitat forta, i la N al costat de la feble.

Cada instància d’una entitat feble està associada amb una única ocurrència de l’entitat forta (per això és en el costat 1 de la interrelació), i així és possible completar-ne la identificació de manera única.

D’altra banda, l’entitat del costat 1 ha de ser obligatòria en la interrelació perquè, si no fos així, alguna instància de l’entitat feble podria no estar associada amb cap de les ocurrències de l’entitat forta i, aleshores, no es podria identificar completament.

Les entitats febles, doncs, no tenen clau primària, però sí un atribut (o un conjunt d’atributs) anomenat discriminant, que permet distingir entre elles totes les instàncies de l’entitat feble que depenen d’una mateixa instància de l’entitat forta.

Tot i no ser un cas gaire freqüent, es poden encadenar entitats febles, de tal manera que una entitat que actuï com a part feble en la interrelació que mantingui amb una altra entitat, pot actuar al mateix temps com a entitat forta respecte a una altra entitat que, al seu torn, la necessiti per identificar completament les seves instàncies.

Addicionalment a la interrelació que els serveix per identificar-se completament, les entitats febles poden participar en altres interrelacions, com qualsevol altra entitat.

Exemple d'entitat feble

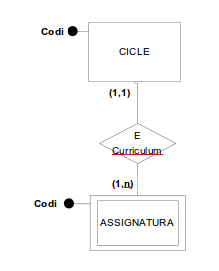
Ha arribat el moment d’establir una clau primària per a l’entitat ASSIGNATURA. Podríem adoptar una codificació derivada de la utilitzada en els currículums oficials: C1, C2, C3, etc. (de Crèdit 1, Crèdit 2, i així successivament). Podríem anomenar aquest atribut CodiAssignatura. Però això no permetria distingir les assignatures dels diferents cicles formatius impartits en el nostre institut.

Per aconseguir la identificació inequívoca de cada crèdit, en primer lloc hauríem de comptar amb una nova entitat anomenada, per exemple, CICLE, per emmagatzemar tots els cicles impartits al centre. Aquesta entitat seria forta, i les seves instàncies es distingirien inequívocament les unes de les altres mitjançant una clau primària que es podria dir CodiCicle.

A continuació, hauríem d’establir una interrelació binària anomenada, per exemple, Curriculum, en la qual participés l’entitat ASSIGNATURA com a entitat feble, en el costat N de la interrelació, i l’entitat CICLE com a entitat forta, en el costat 1.

Les relacions febles en els diagrames ER es representen amb un rectangle de doble línia.

Notació

Per incorporar les entitats febles als diagrames ER, cal aplicar unes poques regles de notació addicionals:

• Les entitats febles es representen escrivint el seu nom en majúscules i en singular, dins d’un rectangle dibuixat amb una línia doble.

• La interrelació que uneix l’entitat feble amb la seva forta es representa amb un rombe també de línia doble.

• Aquest rectangle s’ha d’unir, igualment amb una línia doble, amb la interrelació que l’associa amb la seva entitat forta de la qual depèn.

• L’atribut o el conjunt d’atributs que actuïn com a discriminants han d’anar subratllats amb una línia discontínua.