Diferència entre revisions de la pàgina «ASIX-M3-UF2-A3»

Revisió del 18:15, 25 gen 2024

Introducció

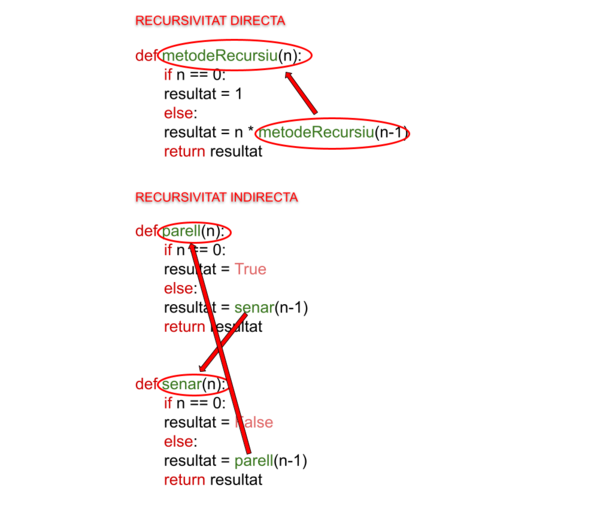
Els programes que hem vist fins ara estan estructurats generalment com a mètodes que es criden entre si, d'una manera disciplinada i jeràrquica. No obstant això, per a alguns problemes és convenient fer que un mètode es cridi a si mateix. Aquest mètode es coneix com a mètode recursiu; aquest mètode es pot cridar en forma directa o indirecta a través d'un altre mètode.

Conceptes de recursivitat

Els mètodes per solucionar problemes recursius tenen diversos elements en comú. Quan es fa una crida a un mètode recursiu per resoldre un problema, el mètode en realitat és capaç de resoldre només el (els) cas(os) més simple(s), o cas(os) base. Si es fa la crida al mètode amb un cas base, el mètode retorna un resultat. Si es fa la crida al mètode amb un problema més complex, el mètode comunament divideix el problema en dues peces conceptuals: una peça que el mètode sap com resoldre i una altra peça que no sap com resoldre. Perquè la recursivitat sigui factible, aquesta última peça ha de ser similar al problema original, però una versió lleugerament més senzilla o simple del mateix. A causa que aquest nou problema s'assembla al problema original, el mètode crida a una nova còpia de si mateix per treballar en el problema més petit; a això se li coneix com crida recursiva, i també com a pas recursiu. En general, el pas recursiu inclou una instrucció return, ja que el seu resultat es combina amb la part del problema que el mètode va saber com resoldre, per formar un resultat que es passarà de tornada al mètode original que va fer la crida. Aquest concepte de separar el problema en dues porcions més petites és una forma del mètode “divideix i venceràs”.

El pas recursiu s'executa mentre segueixi activa la crida original al mètode (és a dir, que no hagi acabat la seva execució). Es poden produir moltes crides recursives més, a mesura que el mètode divideix cada nou subproblema en dues peces conceptuals. Perquè la recursivitat acabi en un moment donat, cada vegada que el mètode es crida a si mateix amb una versió més simple del problema original, la seqüència de problemes cada vegada més petits ha de convergir en un cas base. En aquest punt, el mètode reconeix el cas base i retorna un resultat a la còpia anterior del mètode. Després s'origina una seqüència de tornades, fins que la crida al mètode original retorna el resultat final al mètode que el va cridar.

Un mètode recursiu pot cridar a un altre mètode, que al seu torn pot fer una crida de tornada al mètode recursiu. A aquest procés se li coneix com cridada recursiva indirecta o recursivitat indirecta. Per exemple, el mètode A crida al mètode B, que fa una crida de tornada al mètode A. Això se segueix considerant com recursivitat, a causa que la segona crida al mètode A es realitza mentre la primera segueix activa; és a dir, la primera crida al mètode A no ha acabat encara d'executar-se (a causa que està esperant que el mètode B li retorni un resultat) i no ha tornat al mètode original que va cridar al mètode A.

Per comprendre millor el concepte de recursivitat, vegem un exemple que és bastant comú per als usuaris de computadora: la definició recursiva d'un directori en una computadora. En general, una computadora emmagatzema els arxius relacionats en un directori. Aquest directori pot estar buit, pot contenir arxius i/o pot contenir altres directoris (que, en general, es coneixen com a subdirectoris). Al seu torn, cadascun d'aquests directoris pot contenir també arxius i directoris. Si volem llistar cada arxiu en un directori (incloent tots els arxius en els subdirectoris d'aquest directori), necessitem crear un mètode que llegeixi primer els arxius del directori inicial i que després faci cridades recursives per llistar els arxius en cadascun dels subdirectoris d'aquest directori. El cas base ocorre quan s'arriba a un directori que no contingui subdirectoris. En aquest punt, s'han llistat tots els arxius en el directori original i no es necessita més la recursivitat.

Exemple d'ús de recursivitat: factorials

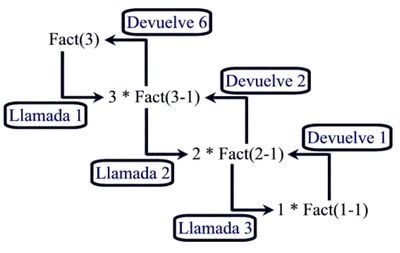
Escrivim un programa recursiu, per realitzar un popular càlcul matemàtic. Considerem el factorial d'un enter positiu n, escrit com a n! (i es pronuncia com a “factorial de n”), que és el producte: n * (n – 1) * (n – 2)* ... * 1

on 1! és igual a 1 i 0! es defineix com 1. Per exemple, 5! és el producte 5 * 4 * 3 * 2 * 1, que és igual a 120.

El factorial de l'enter numero (on numero >= 0) pot calcular-se de manera iterativa (sense recursivitat), usant una instrucció for de la següent manera:

factorial = 1;
for comptador in range(numero, 1, -1):
   factorial *= comptador

Podem arribar a una declaració recursiva del mètode del factorial, si observem la següent relació: n! = n * (n – 1)!

Per exemple, 5! és sens dubte igual a 5 · 4!, com es mostra en les següents equacions:

5! = 5 * 4 * 3 * 2 * 1 5! = 5 * (4 * 3 * 2 * 1) 5! = 5 * (4!)

Per tant podem resoldre el problema de forma recursiva així:

def factorial(n):
   if n <=1:
      # Cas base: Se sap el resultat directament
      return 1
   else: 
    ''' Cas recursiu: Per calcular-lo cal invocar el propi metode
        El valor del nou paràmetre d'entrada ha de variar de manera que
        es vagi aproximant al cas base '''
      return n * factorial(n - 1)

• Si ometem el cas base o escrivim el pas recursiu de forma incorrecta, de manera que no convergeixi en el cas base, es pot produir un error lògic conegut com a recursivitat infinita, on es realitzen crides recursives de forma contínua, fins que s'esgota la memòria. Aquest error és anàleg al problema d'un cicle infinit en una solució iterativa.

Exemple d'ús de recursivitat: sèrie de Fibonacci

La sèrie de Fibonacci, 0, 1, 1, 2, 3, 5, 8, 13, 21, ... comença amb 0 i 1, i té la propietat que cada nombre subsegüent de Fibonacci és la suma dels dos nombres Fibonacci anteriors.

La sèrie de Fibonacci es pot definir de manera recursiva com: fibonacci(0) = 0 fibonacci(1) = 1 fibonacci(n) = fibonacci(n – 1) + fibonacci(n – 2)