M3 - Programació estructurada / Continguts UF2: Disseny modular

Descomposició funcional

• L’objectiu serà resoldre el problema general com a una suma de subproblemes més petits.

• La solució a cada subproblema s’anomena subrutina o subprograma, i a Java, mètode.

• Permet la reutilització del codi, facilita la seva lectura i el seu manteniment.

• Escriure codi més genèric facilita la seva reutilització.

Disseny descendent

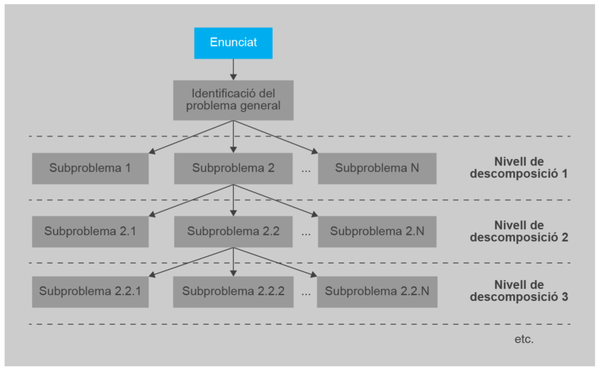
• El mètode del disseny descendent consisteix en descompondre el problema a resoldre en altres més senzills. A aquests se'ls aplica el mateix procediment fins arribar a problemes prou petits que podem resoldre directament.

• Refinament de l’algorisme (stepwise refinement) és com es coneix aquest procediment de descomposició.

• Representació en forma d'arbre:

- Cada node és un mòdul, o problema, o solució hipotètica.

- Cada subarbre depenent d'aquest node es fa servir per a la resolució d'aquest subproblema.

- El node del nivell més alt és el problema de partida.

- L’algorisme serà correcte si la solució que es dóna a cada nivell ho és.

- El programa es pot construir de sota a dalt creant primer procediments que resolguin els mòduls de detall que, un cop comprovats seran utilitzats per altres procediments més generals fins a arribar a la creació del programa.

Reutilització de subproblemes resolts

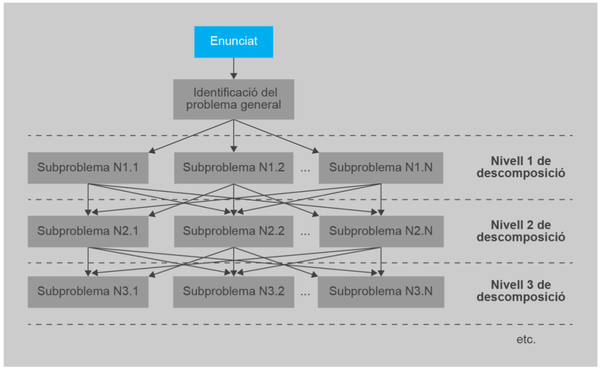
• La descomposició mitjançant disseny descendent permet reaprofitar la solució de subproblemes idèntics, o força semblants.

• Qualsevol subproblema d’un nivell donat pot ser part de qualsevol subproblema d’un nivell superior. Per remarcar

• En descompondre un problema, s'ha d'intentar fer-ho de manera que es forci l’aparició de subproblemes repetits, i així la seva resolució es pot reaprofitar en diversos llocs.

Aplicació correcta del disseny descendent

Diferents persones poden arribar a conclusions diferents sobre com dur a terme la descomposició. Entre totes les solucions diferents possibles, algunes es poden considerar millors que d’altres. De fet, res impedeix, partir d'una solució concreta i aplicar refinaments que la millorin.

Criteris per a l'avaluació de la descomposició:

• Si un problema que sembla a priori força complex es descompon en molts pocs nivells, potser val la pena fer una segona ullada. Inversament, si un problema no massa complex té massa nivells, potser s’ha anat massa lluny en la descomposició.

• Veure si el nombre de passes incloses a cadascun dels subproblemes no és excessivament gran i és fàcil de seguir i entendre. En cas contrari, potser encara faria falta aplicar nous nivells de descomposició.

• Repassar que els noms assignats als subproblemes siguin autoexplicatius i expressin clarament la tasca que estan resolent. Sense ni tan sols llegir les seves passes, caldria entendre perfectament què s’assoleix en resoldre’ls. En cas contrari, potser la descomposició no està agrupant conjunts de passes realment relacionades entre elles.

• Si absolutament cap dels subproblemes és reutilitzat enlloc, especialment en descomposicions en molts nivells, és molt possible que no s’hagi triat correctament la manera de descompondre alguns subproblemes.

• Vinculat al punt anterior, l’aparició de subproblemes molt semblants o idèntics, però tractats per separat en diferents llocs, també sol ser indici que no s’està aplicant la capacitat de reutilitzar subproblemes correctament.