M2 - Bases de dades / UF1NF3: Normalització
El disseny d’una base de dades pot ser una tasca extremadament complexa. Hi ha diferents metodologies que permeten abordar el problema de trobar l’esquema relacional que representi millor la realitat que es vol modelitzar.
Coneixem el model Entitat-Relació per establir models per a qualsevol realitat, del qual s’obté, com a resultat, el diagrama Entitat-Relació, altrament anomenat diagrama de Chen. També coneixem el procés de traducció d’un diagrama Entitat-Relació a un esquema relacional.
Per tant, si per arribar a l’esquema relacional que ha de modelitzar la realitat hem seguit el camí que consisteix a, primerament, efectuar el diagrama Entitat-Relació per després efectuar-ne la traducció al model relacional, i el diagrama Entitat-Relació era correcte, haurem obtingut un esquema relacional del tot correcte. Aquest seria el camí aconsellable.
Però no sempre és així i ens trobem dissenys efectuats directament en l’esquema relacional. Hi ha diferents causes que ho provoquen:
- D’entrada, el model Entitat-Relació és posterior al model relacional i, per tant, hi ha bases de dades que van ser formulades directament en la terminologia relacional. No hi havia cap altra opció!
- Hi ha dissenyadors que “no volen perdre el temps” en un model Entitat-Relació i dissenyen directament en el model relacional. Quin error més gran!
- De vegades, s’ha de modificar la base de dades a causa de noves necessitats, i el disseny s’efectua directament sobre aquesta en lloc d’analitzar-se i realitzar-se sobre el model Entitat-Relació per després transferir els canvis a l’esquema relacional. Quin error més gran!
Fixeu-vos que donem un suport absolut al fet d’utilitzar el model Entitat-Relació per obtenir-ne posteriorment el model relacional. Un bon disseny en el model Entitat-Relació acostuma a proporcionar una base de dades relacional ben dissenyada, cosa que no passarà si el disseny Entitat-Relació incorpora errors. D’altra banda, si no hi ha hagut el disseny Entitat-Relació previ, hi ha més possibilitats de tenir una base de dades relacional mal dissenyada.
La teoria de la normalització és un mètode que permet assegurar si un disseny relacional (tant si
prové de la traducció d’un diagrama Entitat-Relació com si s’ha efectuat directament en el model
relacional) és més o menys correcte.
En general, els mals dissenys poden originar les situacions següents:
- Repetició de la informació
- Impossibilitat de representar certa informació:
- Anomalies en les insercions
- Anomalies en les modificacions
- Anomalies en els esborraments
Un bon disseny ha d’aconseguir el següent:
- Emmagatzemar tota la informació necessària amb el mínim d’informació redundant.
- Mantenir el mínim de lligams entre les relacions de la base de dades per tal de facilitar-ne la utilització.
- Millorar la consultabilitat de les dades emmagatzemades.
- Minimitzar els problemes d’actualització (altes, baixes i modificacions) que poden sorgir en haver d’actualitzar simultàniament dades de diferents relacions.
Exemple de disseny relacional inadequat
Considerem el disseny relacional de la taula següent per enregistrar la informació dels professors amb els
alumnes de cadascun i la qualificació que han obtingut en els diversos crèdits.
Taula Exemple de disseny relacional inadequat
DniProf NomProfessor DniAlum NomAlumne Edat Credit Nota
__________________________________________________________________________________
33.333.333 Joan Finestra 77.777.777 Anna Taula 20 ADBD 4.5
33.333.333 Joan Finestra 88.888.888 Miquel Cadira 19 ADBD 5.7
33.333.333 Joan Finestra 77.777.777 Anna Taula 20 SGBD 6
33.333.333 Joan Finestra 88.888.888 Miquel Cadira 19 SGBD 7
44.444.444 Maria Porta 77.777.777 Anna Taula 20 MET 6
44.444.444 Maria Porta 88.888.888 Miquel Cadira 19 MET 5
44.444.444 Maria Porta 77.777.777 Anna Taula 20 LLC 4
44.444.444 Maria Porta 88.888.888 Miquel Cadira 19 LLC 3
Oi que convindreu que aquest disseny està pensat amb els peus? Ràpidament, hi veiem els
problemes següents:
* Hi ha informació repetida, fet que pot provocar inconsistències. Fixem-nos que en cas
d’haver de modificar qualsevol dels valors dels camps que formen la clau primària (DniProf,
NomProfessor, DniAlum, NomAlumne, Edat, Credit), el canvi s’ha d’efectuar en totes les
files en què apareix aquest valor.
* No hi pot haver valors nuls en les columnes que formen la clau primària.
* Així, si no coneixem l’edat d’un alumne, tenim un greu problema.
* En cas d’arribar a la conclusió que necessitem emmagatzemar més informació dels professors
o dels alumnes, caldrà afegir més columnes i repetir la informació per a cada fila en què
aparegui el professor o alumne.
* Consultar la informació pot esdevenir feixuc atesa la gran quantitat d’informació diferent
que conté.
El mètode que proposa la teoria de la normalització per determinar si un disseny relacional és correcte consisteix a avaluar el disseny de totes les relacions (taules) per tal de veure en quin grau de normalitat es troba cadascuna i, així, poder decidir si el disseny ja és correcte o si cal refinar-lo.
La teoria de la normalització defineix les formes normals com a indicadors per avaluar el grau de
normalitat de les relacions, i es diu que una relació està en una forma normal determinada quan
satisfà un conjunt determinat de condicions.
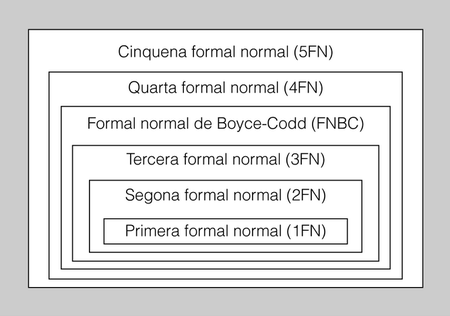
Hi ha diferents graus de normalitat i, per tant, de formes normals, les quals compleixen la relació d’inclusió de la figura següent, que s’ha d’interpretar en el sentit que a mesura que augmenta el nivell de la forma normal, la relació ha de complir un conjunt de condicions més restrictiu i, per tant, continua verificant les condicions de les formes normals de nivell inferior.
Figura Relació d’inclusió entre les diverses formes normals
Així, doncs, l’objectiu hauria de ser aconseguir un esquema relacional en què totes les relacions tinguessin el grau màxim de normalitat, és a dir, en què totes es trobessin en la cinquena forma normal (5FN).
El procés de normalització per aconseguir que una relació que es troba en una forma normal X passi
a estar en una forma normal Y superior a X consisteix sempre en la descomposició o subdivisió de la
relació original (forma normal X) en dues o més relacions que verifiquin el nivell de forma normal Y.
Per tant, el procés de normalització augmenta el nombre de relacions presents en la base de dades. Amb això, segur que s’aconsegueix una disminució de redundàncies i una disminució de les anomalies en els problemes d’actualització de la informació, però, en canvi, es penalitzen les consultes, ja que la seva execució haurà d’anar a cercar la informació en moltes taules relacionades entre elles.
Així, doncs, cal trobar un equilibri, i de vegades pot ser convenient renunciar al nivell màxim de normalització (5FN) i, per tant, permetre una certa redundància en els esquemes amb la finalitat d’alleugerir els costos de les consultes. En aquestes situacions, es parla d’un procés de desnormalització.
El nostre objectiu final és conèixer les condicions que han de complir les relacions per assolir cadascun dels nivells de forma normal, i el procés per dividir les relacions en noves relacions que verifiquin les condicions desitjades. Per aconseguir-ho, hem de conèixer els conceptes de relació universal i dependència funcional.
Contingut
La relació universal
En efectuar directament el disseny relacional d’una base de dades, el dissenyador es troba amb un conjunt de conceptes que tradueix en atributs, els quals, pel seu significat, agruparà en una o més relacions.
Anomenem relació universal la relació consistent en l’agrupament dels atributs corresponents a tots
els conceptes que constitueixen una base de dades relacional.
Taula Relació universal per a un esquema relacional ideat per a una gestió de comandes de compra
Num DataComanda Article Descripcio Qtat Preu DataPrevista NomProv PaisProv Moneda
22.523 25-05-2000 PC3-500 PC Pentium III a 500 5 150 1-06-2000 ARKANSAS XINA EUR
22.523 25-05-2000 PRO-15 Protector pantalla 15” 5 8 1-06-2000 ARKANSAS XINA EUR
22.524 27-05-2000 PC3-500 PC Pentium III a 500 15 145 5-06-2000 MELISSA ITÀLIA USD
22.524 27-05-2000 PRO-15 Protector pantalla 15” 15 50 5-06-2000 MELISSA ITÀLIA USD
22.525 27-05-2000 INK430 Cartutx de tinta 430 20 25 31-5-2000 ARKANSAS XINA EUR
Així, imaginem que es vol dissenyar una base de dades per al control de les comandes de compra d’una organització determinada. Imaginem que cal incloure-hi els conceptes corresponents a número i data de la comanda; codi, descripció, quantitat i preu pactat per cada article sol·licitat; data prevista de lliurament de la comanda; nom (NomProv) i país (PaisProv) del proveïdor; i moneda en què es pacta la comanda. La relació universal es representa en la taula anterior.
Oi que hi ha molta redundància i poca organització? Evidentment, el disseny relacional d’una base de dades basat en la relació universal acostuma a ser del tot incorrecte, i fa necessari aplicar un procés de normalització per tal d’anar dividint la relació en altres relacions de manera que assoleixin graus de normalitat millors, és a dir, compleixin les restriccions corresponents a les formes normals més elevades.
Molt poques vegades es parteix de la relació universal. L’experiència dels dissenyadors provoca que, d’entrada, ja es pensi en relacions que assoleixen un cert grau de normalitat.
Dependències funcionals
Les definicions de les diferents formes normals, és a dir, el conjunt de condicions que les defineixen, es basen en el concepte de dependència funcional.
Donats dos atributs (o conjunts d’atributs) A i B d’una relació R, direm que B depèn funcionalment
de A si per cada valor de A existeix un, i només un, valor de B associat amb ell. També direm que
A implica B. Ho simbolitzarem per A –> B.
El concepte de dependència funcional estableix lligams entre atributs o conjunt d’atributs d’una mateixa relació.
Taula Relació universal per a un esquema relacional ideat per a una gestió de comandes de compra
Num DataComanda Article Descripcio Qtat Preu DataPrevista NomProv PaisProv Moneda
22.523 25-05-2000 PC3-500 PC Pentium III a 500 5 150 1-06-2000 ARKANSAS XINA EUR
22.523 25-05-2000 PRO-15 Protector pantalla 15” 5 8 1-06-2000 ARKANSAS XINA EUR
22.524 27-05-2000 PC3-500 PC Pentium III a 500 15 145 5-06-2000 MELISSA ITÀLIA USD
22.524 27-05-2000 PRO-15 Protector pantalla 15” 15 50 5-06-2000 MELISSA ITÀLIA USD
22.525 27-05-2000 INK430 Cartutx de tinta 430 20 25 31-5-2000 ARKANSAS XINA EUR
En la relació universal de la taula anterior diríem que, entre d’altres, la data de comanda depèn funcionalment del número de comanda, igual que la data prevista, el nom i el país del proveïdor i la moneda. Ho podríem escriure com segueix:
Num –> DataComanda
Num –> DataPrevista
Num –> NomProv
Num –> PaisProv
Num –> Moneda
En tractar-se de diferents atributs que depenen funcionalment d’un mateix atribut, escriurem:
Num –> DataComanda, DataPrevista, NomProv, PaisProv, Moneda
Donats dos atributs (o conjunts d’atributs) A i B d’una relació R, direm que B té una dependència
funcional completa o total de A si B depèn funcionalment de A però no depèn funcionalment de cap
subconjunt de A.
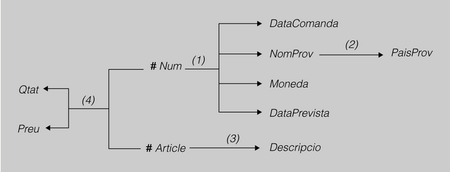
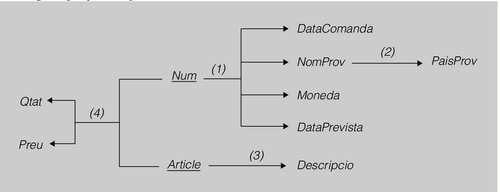
És molt convenient representar les dependències funcionals d’una relació mitjançant un esquema de dependències funcionals. L’esquema per a la relació universal de seria el que es mostra en la figura següent.
Figura Exemple d’esquema de dependències funcionals
Fixem-nos que hem marcat els atributs que són clau d’alguna de les entitats que formen part de la relació: Article identifica l’article i Num identifica la comanda. Fixem-nos, també, que la parella (Num, Article) identifica la quantitat i preu dels articles demanats en la comanda.
En aquest esquema, es poden veure les dependències funcionals entre els atributs. Es veu que DataComanda, NomProv, Moneda i DataPrevista depenen funcionalment (1) de Num, que PaisProv depèn funcionalment (2) de NomProv, i que Descripció depèn funcionalment (3) d’Article. Així mateix, QtatiPreu depenen funcionalment (4) de Num i Article.
És evident que les dependències (1), (2) i (3) són totals, ja que la part esquerra de la dependència (l’implicador) està formada per un únic atribut i, per tant, és impossible que la part dreta de la dependència (l’implicat) pugui dependre d’un subconjunt de l’implicador. La dependència (4) també és total, ja que Qtat i Preu depenen de la parella (Num, Article) i no pas de cap subconjunt d’aquesta.
Una darrera apreciació sobre la dependència funcional (4) de la figura anterior: veiem que en una mateixa comanda (Num) no és possible tenir diverses vegades el mateix article (Article), ja que els atributs Qtat i Preu depenen funcionalment de (Num, Article). En cas que fos necessari tenir diverses vegades el mateix article en una comanda, caldria utilitzar algun altre atribut per identificar l’article dins la comanda com, per exemple, el NumeroDeLinia de la comanda.
Donat un atribut o conjunt d’atributs A d’una relació, direm que A és un determinant de la relació
si hi ha algun altre atribut o conjunt d’atributs B que té dependència funcional total de A.
En el cas anterior, veiem que Num, Article, NomProv i la parella (Num, Article) són determinants de la relació.
Donats A, B i C atributs o conjunts d’atributs d’una relació, direm que C depèn transitivament de A
a través de B si B depèn funcionalment de A, C depèn funcionalment de B, i A no depèn funcionalment
de B.
En l’exemple anterior, podem dir que PaisProv depèn transitivament de Num a través de NomProv.
Primera forma normal
En aplicar el procés de normalització a una relació, es comença per comprovar si la relació està en primera forma normal i, si no és el cas, s’efectuen les modificacions oportunes per aconseguir-ho.
Una relació està en primera forma normal (1FN) si cap atribut pot contenir valors no atòmics (indivisible).
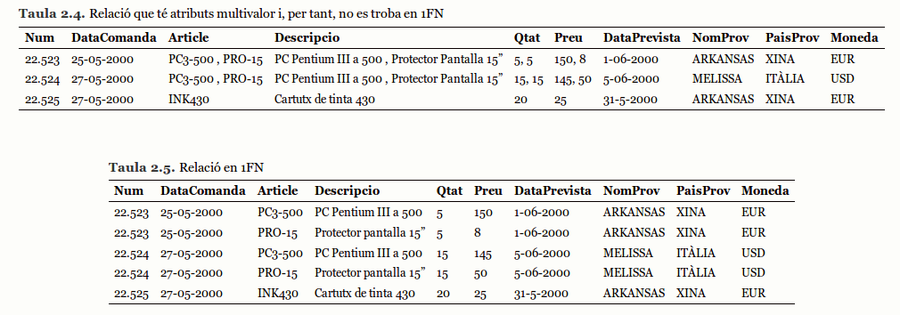
Considerem la relació universal de la taula.4.
La relació de la taula.4 no està en 1FN, ja que té atributs que poden contenir més d’un valor. Veiem que aquest exemple inclou tres files (comandes 22.523, 22.524 i 22.525), i alguns atributs (Article, Descripcio, QtatiPreu) tenen diversos valors per a algunes de les files.
El procés que s’ha de seguir per assolir una 1FN és afegir tantes files com sigui necessari per a
cadascun dels diferents valors del camp o camps que tinguin valors no atòmics.
Així, en el nostre cas, obtenim la relació en 1FN de la taula.5.
De fet, la restricció que persegueix la 1FN forma part de la definició del model relacional i, per tant, tota relació, per definició, ha d’estar en 1FN. És a dir, aquesta forma normal és redundant amb la definició del model relacional i no caldria considerar-la. Es manté, però, per assegurar que les relacions dissenyades tenen un punt de partida correcte.
En general, les relacions en 1FN poden tenir molta informació redundant. Això no ens ha de preocupar, ja que la solució rau en les formes normals de nivell superior.
Preservació d'informació i dependències en la normalització
Natural Join de R1*R2
L’operació de Natural Join és la combinació de totes les dades de la primera relació (R1) amb totes les
de la segona (R2), sempre que els valors de les dades de les columnes anomenades de forma idèntica a les
dues relacions coincideixin.
En el procés de normalització d’una relació R s’apliquen processos de descomposició per aconseguir relacions R1, R2, …, Rn que verifiquin un nivell de normalització superior al de la relació R. La descomposició consisteix a efectuar projeccions de la relació R sobre atributs que verifiquen certes condicions, la qual cosa dóna lloc a l’aparició de R1, R2, …, Rn.
Cal garantir que la descomposició de R en R1, R2, …, Rn preservi la informació existent, és a dir, que el natural-join R1 * R2 * … * Rn proporcioni exactament la mateixa informació que tenia la relació R original, tant enintensió (quantitat d’atributs) com en extensió (quantitat de files).
De la mateixa manera caldria garantir la conservació de les dependències, és a dir, el conjunt de dependències associades a la relació R original ha de ser equivalent al conjunt de dependències associat a les relacions R1, R2, …, Rn.
Ja podem avançar que la conservació de les dependències no es pot garantir en tots els processos de normalització.
Segona forma normal
La segona forma normal persegueix l’eliminació dels problemes motivats per la presència de dependències funcionals no totals dels atributs que no formen part de la clau primària respecte a la clau primària.
Una relació està en segona forma normal (2FN) si està en 1FN i tot atribut que no pertany a la clau té
dependència funcional total de la clau.
Considerem la relació següent en 1FN ideada per a la gestió de comandes de compra en una organització:
R (__Num__, DataComanda, __Article__, Descripcio, Qtat, Preu, DataPrevista, NomProv, PaisProv, Moneda)
Veiem que la clau primària està formada per la parella (Num, Article) i que, en l’esquema de dependències funcionals associat (figura 2.3), hi ha atributs fora de la clau primària que no tenen dependència funcional completa de la clau.
En efecte, les dependències funcionals (1), (2) i (3) ens presenten atributs que no tenen dependència funcional total de la clau, formada per la parella (Num, Article).
El procés que s’ha de seguir per assolir una 2FN és dividir la relació (conservant la informació i les dependències)
en tantes relacions com sigui necessari de manera que cada relació verifiqui que els seus atributs no-clau tenen
dependència funcional total de la clau.
L’esquema de dependències funcionals ajuda a veure les relacions que han d’aparèixer. Així, en el nostre cas, de les dependències (1), (3) i (4) obtenim les relacions en 2FN:
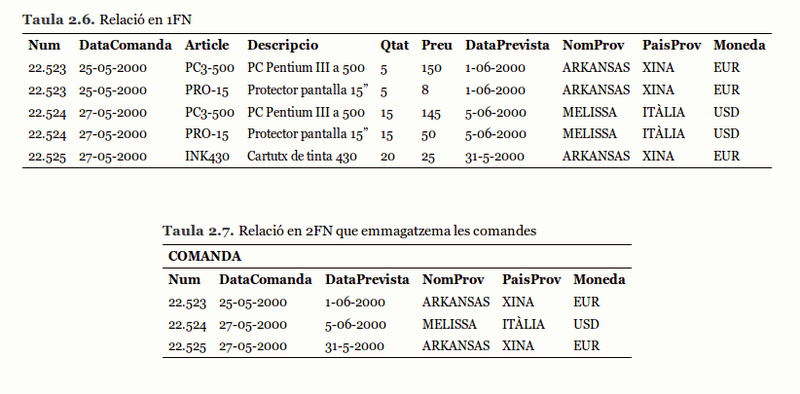
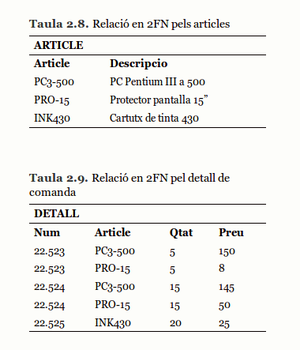
COMANDA (__Num__, DataComanda, DataPrevista, Moneda, NomProv, PaisProv)
ARTICLE (__Article__, Descripcio)
DETALL (__Num__, __Article__, Qtat, Preu)
comanda article
És molt probable que aquest disseny fos el proposat com a punt de partida, és a dir: sovint, en efectuar un disseny ja obtindrem relacions que estan en 2FN i, fins i tot, en formes normals de nivell superior.
La informació que hi ha en la taula 2.6 corresponent a la relació que acabem de normalitzar ara passa a estar repartida en tres taules (taula 2.7, taula 2.8 i taula 2.9).
Per acabar, fixem-nos que amb el nou disseny s’ha aconseguit eliminar molta redundància i, per tant, es redueixen els problemes en les operacions d’actualització i consulta. Però no desapareixen tots.
Tercera forma normal
Considerem el disseny de les relacions següents en 2FN ideades per a la gestió de les comandes de compra d’una organització:
COMANDA (__Num__, DataComanda, DataPrevista, Moneda, NomProv, PaisProv)
ARTICLE (__Article__, Descripcio)
DETALL (__Num__, __Article__, Qtat, Preu)
comanda article
Fixem-nos que el país del proveïdor apareix en cada comanda. Si partim de la base que el país on resideix el proveïdor és únic, oi que encara hi ha informació redundant?
La tercera forma normal persegueix l’eliminació dels problemes motivats per la presència de dependències transitives dels atributs que no formen part de la clau primària, respecte de la clau primària.
Una relació està en tercera forma normal (3FN) si està en 2FN i cap atribut que no pertany
a la clau depèn transitivament de la clau.
Les relacions ARTICLE i DETALL que ens ocupen ja estan en 3FN, però considerem la relació comanda que conté el país del proveïdor.
COMANDA (__Num__, DataComanda, DataPrevista, Moneda, NomProv, PaisProv)
L’atribut PaisProv depèn transitivament de Num a través de NomProv. Per tant, aquesta relació no està en 3FN.
El procés que s’ha de seguir per assolir una 3FN és dividir la relació (conservant la informació
i les dependències) en noves relacions més simples, de manera que cada relació verifiqui que cap
dels seus atributs no-clau depèn transitivament de la clau.
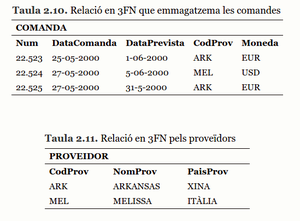
En el nostre cas, obtenim les relacions en 3FN:
PROVEIDOR (__CodProv__, NomProv, PaisProv)
COMANDA (__Num__, DataComanda, DataPrevista, Moneda, CodProv)
proveïdors
Fixem-nos que, en trencar la relació inicial COMANDA, ha semblat oportú considerar un nou atribut (CodProv) que identifiqui millor la nova relació PROVEÏDOR. Aquest fet no és imprescindible i no sempre serà convenient. Podríem haver considerat el trencament següent:
PROVEIDOR (__NomProv__, PaisProv)
COMANDA (__Num__, DataComanda, DataPrevista, Moneda, NomProv)
proveïdors
Ara bé, per a aquesta darrera possibilitat hem escollit el nom del proveïdor com a clau primària de la nova relació PROVEIDOR, i l’experiència ens aconsella definir un codi que ens permeti identificar-los de manera més clara que la que proporciona el seu nom.
Tenint en compte el disseny que incorpora l’atribut CodProv, tindríem la conversió de la taula 2.7 en la taula 2.10 i taula 2.11.
Forma normal de Boyce-Codd
Considerem les naus d’emmagatzematge que hi ha en un gran mercat dedicades a guardar les mercaderies dels venedors del mercat. Imaginem que cada nau guarda mercaderia d’un tipus concret (carn fresca, peix fresc, congelats, vegetals, basar…) i que cada venedor pot dipositar mercaderia en diferents naus segons el tipus de mercaderia de cada nau (una parada de peix del mercat es pot dedicar a vendre peix fresc i peix congelat, per exemple). Ara bé, tota la mercaderia d’unes mateixes característiques d’un venedor es troba concentrada en una ubicació dins una mateixa nau per minimitzar al màxim els desplaçaments del venedor.
Per tenir constància de quin tipus de material hi ha a cada nau, es dissenya aquesta relació:
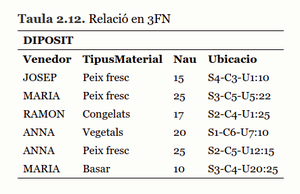
DIPOSIT (__Venedor__, __TipusMaterial__, Nau, Ubicacio)
La taula 2.12 ens exemplifica la situació. Fixem-nos que es troba en 3FN:
- Tots els atributs no pertanyents a la clau (Nau i Ubicacio) tenen dependència funcional total de la clau (2FN).
En efecte, la Nau i la Ubicacio dins la nau depenen del Venedor i del TipusMaterial, ja que hi pot haver diverses naus dedicades a un tipus de material, però tot el material similar d’un venedor es troba en una nau determinada. Al mateix temps, hi pot haver diverses naus amb material d’un venedor a causa de la diferent tipologia del material.
- Cap atribut no pertanyent a la clau (Nau i Ubicacio) no depèn transitivament de la clau. En efecte, és impossible que hi hagi cap dependència transitiva de la clau, ja que no hi ha cap atribut que pugui servir de pont per a la transitivitat. Però aquesta relació, tot i estar en 3FN, presenta anomalies:
- Si en un moment donat una nau no té material de cap venedor, es perd la informació referent al tipus de mercaderia que correspon a la nau.
- Si canvia la descripció del tipus de mercaderia assignada a una nau, cal modificar tantes files com venedors amb dipòsits d’aquell tipus de mercaderia hi hagi a la nau.
Una relació està en la forma normal de Boyce-Codd (FNBC) si està en 2FN i tots els seus
determinants són claus candidates.
L’anterior relació DIPOSIT no es troba en FNBC, ja que l’atribut Nau és un determinant de la relació i TipusMaterial té dependència funcional total de Nau, i en canvi Nau no és clau candidata.
És a dir, es dóna aquesta situació:
Nau –> TipusMaterial
Es verifica que tota relació en FNBC està en 3FN però no a l’inrevés, com hem pogut comprovar en el nostre cas.
El procés que s’ha de seguir per assolir una FNBC és apartar de la relació els atributs que depenen
dels determinants que no són claus candidates, i formar noves relacions que recullen els atributs
apartats i que preserven la informació inicial.
En el nostre cas, apartarem de la relació l’atribut TipusMaterial i obtindrem les relacions en FNBC:
DIPOSIT (__venedor__, nau, ubicacio)
nauTipus
NAU_TIPUS (__nau__, tipusMaterial)
En els trencaments efectuats sobre una relació no normalitzada per assolir relacions 2FN i 3FN, cal efectuar la divisió de manera que es preservin la informació i les dependències funcionals, fet sempre possible en el pas a 2FN i 3FN. En el pas a FNBC, també sempre és possible efectuar la divisió mantenint la informació, però no sempre és possible el manteniment de les dependències funcionals.
En el nostre cas, la relació inicial DIPOSIT contenia les dependències funcionals següents:
Venedor, TipusMaterial –> Nau, Ubicacio
Nau –> TipusMaterial
I, en les relacions finals DIPOSITS i NAU_TIPUS, s’ha perdut la dependència funcional que indicava que la Nau depenia de la parella Venedor i TipusMaterial:
DIPOSIT: Venedor –> Nau, Ubicacio
NAU_TIPUS: Nau –> TipusMaterial
La dependència funcional s’ha perdut perquè el concepte de dependència funcional en el model relacional es defineix únicament entre atributs d’una mateixa relació, i en aquest s’hauria de poder definir entre atributs de relacions diferents. De tota manera, el concepte d’integritat referencial intenta superar aquesta limitació.
A causa de la pèrdua de dependències funcionals, que no sempre es produeix, sovint no es normalitza a FNBC i es treballa amb relacions en 3FN.
Quarta forma normal
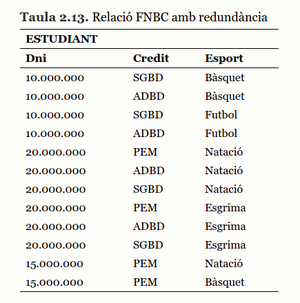
Considerem la relació ESTUDIANT (taula 2.13) dissenyada per emmagatzemar els diversos crèdits que cursa i les diverses activitats esportives que practica.
ESTUDIANT(__Dni__, __Credit__, __Esport__)
És a dir, la relació estudiant recull la possibilitat que un estudiant cursi diversos crèdits i practiqui diverses activitats esportives.
Aquesta relació es troba en FNBC i, tot i així, hi ha redundància, provocada per un nou concepte: les dependències multivalents.
Donats A i B atributs o conjunts d’atributs d’una relació, direm que B té una dependència
multivalent de A si un valor de A pot determinar un conjunt de valors de B. Ho simbolitzarem
amb la notació A –» B.
Les dependències multivalents no són dependències funcionals. En canvi, però, una dependència funcional es pot arribar a considerar una dependència multivalent en què per cada valor de l’implicant hi ha un únic valor de l’implicat.
Els problemes provocats per les dependències funcionals han causat la definició de la 1FN, 2FN, 3FN i FNBC. La redundància provocada per les dependències multivalents ens porten a definir la 4FN.
Una relació es troba en quarta forma normal (4FN) si està en 3FN i l’implicant de tota
dependència multivalent és una clau candidata.
Quan té lloc una dependència multivalent A –» B, també existeix la dependència multivalent A –» X - (A U B), on X indica el conjunt de tots els atributs de la relació. És a dir, les dependències multivalents es presenten per parelles.
En el nostre cas (taula 2.13) es verifica el següent:
Dni –> Credit
Dni –> Esport
Per assolir la 4FN a partir d’una relació R (A, B, C) que té una dependència multivalent A –» B,
cal descompondre la relació R en dues relacions R1 (A, B) i R2 (A, C).
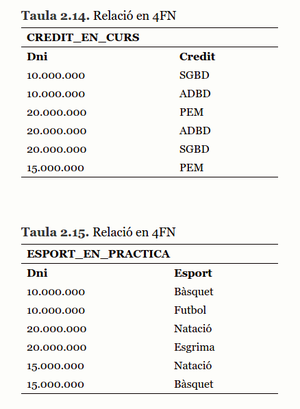
En aquest cas, obtenim les relacions següents (taula 2.14 i taula 2.15):
CREDIT_EN_CURS (__Dni, Credit__)
ESPORT_EN_PRACTICA (__Dni, Esport__)
Sovint, la descomposició causada per les dependències multivalents s’efectua abans de les descomposicions per assolir els nivells 2FN, 3FN i FNBC. En aquesta situació, en les relacions obtingudes, cal aplicar les comprovacions per aconseguir que estiguin en 2FN, 3FN i FNBC.
Cinquena forma normal
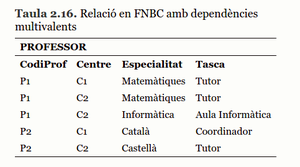
Considerem la relació PROFESSOR (taula 2.16) dissenyada per gestionar els professors d’una determinada institució escolar que té diferents centres de docència. Cada professor està autoritzat a impartir unes determinades especialitats docents que pot posar en pràctica en qualsevol dels centres docents de la institució escolar. Així mateix, cada professor pot exercir, a més de la docència, diferents tasques (càrrecs, tutoria pedagògica, tutoria tècnica…) en diversos centres de la institució escolar.
PROFESSOR (__CodiProf, Centre, Especialitat, Tasca__)
Aquesta relació és FNBC i s’hi aprecia una espècie de dependència multivalent, la qual no es pot solucionar per la via de la descomposició. En efecte, és molt fàcil pensar en una descomposició en les tres relacions següents (exemplificades en la taula 2.17, taula 2.18 i taula 2.19):
CENTRE_DE_PROFESSOR (__CodiProf, Centre__)
ESPECIALITAT_DE_PROFESSOR (__CodiProf, Especialitat__)
TASCA_DE_PROFESSOR (__CodiProf, Tasca__)
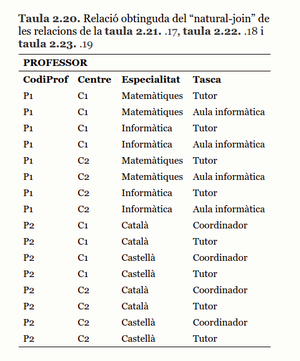
Aquesta descomposició és errònia, ja que si apliquem el natural-join de les tres relacions (taula 2.17, taula 2.18 i taula 2.19) no obtenim la relació inicial (taula 2.16) sinó que obtenim una relació (taula 2.20) amb moltes més instàncies.
Queda clar, doncs, que el mètode utilitzat en aquest cas no és correcte i això és degut al fet que, en aquesta situació, hi ha el que s’anomena dependències mútues entre els atributs de la relació. Les dependències mútues provoquen que la descomposició de la relació en altres relacions (projeccions de l’original) no verifiqui que el seu natural-join coincideix amb la relació original.
Direm que una relació R descomposta en relacions R1, R2, …, Rn satisfà una dependència de
reunió, també anomenada dependència de projecció-join, respecte a R1, R2, …, Rn únicament
si R és igual al natural-join de R1, R2, …, Rn. La notarem com a DR*(R1, R2, …, Rn).
Tornem a l’exemple de descomposició anterior: la relació PROFESSOR s’ha descompost en tres relacions, CENTRE_DE_PROFESSOR,ESPECIALITAT_DE_PROFESSOR i TASCA_DE_PROFESSOR, i hem pogut comprovar que la relació professor no satisfà una dependència de reunió respecte a CENTRE_DE_PROFESSOR, ESPECIALITAT_DE_PROFESSOR i TASCA_DE_PROFESSOR.
Ens cal trobar una dependència de reunió per a la relació PROFESSOR, és a dir, trobar una descomposició tal que el seu natural-join recuperi la relació original. Fixem-nos en la descomposició següent (taula 2.21, taula 2.22 i taula 2.23):
PROFESSOR (__CodiProf, Centre, Especialitat, Tasca__)
PCE = PROFESSOR [__CodiProf, Centre, Especialitat__]
PCT = PROFESSOR [__CodiProf, Centre, Tasca__]
PET = PROFESSOR [__CodiProf, Especialitat, Tasca__]
On PCE, PCT i PET són seccions de la taula original.
En aquesta situació, veiem que si efectuem el natural-join de les tres relacions PCE, PCT i PET obtenim la relació original.
Direm que una relació està en cinquena forma normal (5FN), també anomenada forma normal
projecció-join (FNPJ), si està en 4FN i tota dependència de reunió és conseqüència de
claus candidates.
Per tant, la relació PROFESSOR del nostre exemple no es troba en 5FN, ja que hem trobat la dependència de reunió PROFESSOR*(PCE, PCT, PET) en què les relacions PCE, PCT i PET no estan constituïdes per claus candidates de PROFESSOR.
PCE (__CodiProf, Centre, Especialitat__)
PCT (__CodiProf, Centre, Tasca__)
PET (__CodiProf, Especialitat, Tasca__)
Desnormalització
Pot semblar estrany plantejar-se la desnormalització d’una base de dades, després d’argumentar substancialment la importància que té disposar de bases de dades normalitzades, però en alguns casos una desnormalització controlada pot ser molt útil i, fins i tot, desitjable.
La desnormalització és pot definir com la introducció de redundàncies de forma controlada
en una bases de dades, per tal de fer més eficients alguns processos que, altrament, farien
que globalment el rendiment del sistema resultés poc òptim.
Tot i que per a un sistema donat, es podrien preveure certes modificacions sobre la BD per tal de millorar el rendiment una vegada en funcionament, el més típic és detectar aquestes necessitats a posteriori. Així, doncs, aquests tipus de modificacions sobre la base de dades es duen a terme, habitualment, després d’haver observat certes ineficiències en algunes operacions habituals sobre una base de dades.
A continuació es descriuen algunes situacions, a mode d’exemple, on pot ser útil la desnormalització:
Trigger
Un trigger és un procediment de BD que s’executa automàticament
quan s’esdevenen situacions donades. Per exemple, inserció d’un
nou registre en una taula, modificació d’una dada en un camp donat,
d’una taula, etc.
- En BD on hi ha consultes intensives sobre dades d’una taula que tenen referenciades altres taules on s’hi emmagatzemen descripcions, en algun cas pot ser útil mantenir la descripció en la mateixa taula original, per tal de fer més ràpida la consulta mencionada. Pensem, per exemple, en una taula d’adreces d’empleats que té el codi de la província i que fa referència a una altra taula que té la descripció de la província. Cada cop que calgui consultar la província dels empleats caldrà processar l’operació de join de les dues taules. En canvi, si es disposa del nom de la província en la taula d’adreces, s’evitarà aquesta operació que resulta costosa.
- Afegir camps que són calculables, com ara el total d’una factura, pot reduir, també, el temps de consulta de dades d’aquesta taula, per exemple.
La introducció de redundàncies que desnormalitzin la BD habitualment va lligat a la implementació de certs mecanismes que intenten solucionar els possibles problemes que es podrien generar d’aquestes accions. La forma més típica de controlar els canvis per a evitar inconsistències en en aquests casos és la programació de triggers. Així doncs, es pot programar un trigger, per exemple, perquè en inserir, modificar o eliminar una línia de factura, es recalculi i actualitzi l’import del total de la factura, per així tenir aquest camp calculat sempre consistent.