M2 - Bases de dades / UF1NF3: Model relacional
El model relacional és un model de dades basat en dues disciplines matemàtiques: la lògica
de predicats i la teoria de conjunts.
SGBD
Acrònim de Sistema Gestor de Bases de Dades. És un programari
especialitzat en la gestió de bases de dades (enteses, aquestes,
com un conjunt estructurat d’informació).
Potser a causa d’aquest sòlid fonament teòric, que proporciona a aquest model una robustesa excepcional, els SGBD relacionals (o SGBDR) són actualment els que tenen una implantació més gran en el mercat. El model relacional va ser proposat originàriament per Edgar Frank Codd en el seu treball A Relational Model of Data for Large Shared Data Banks (‘Un model relacional de dades per a grans bancs de dades compartits’) l’any 1970, tot i que no es va implementar comercialment fins al final de la dècada.
E. F. Codd
Codd treballava per a IBM, però no va ser aquesta multinacional qui va creure abans en les
possibilitats del model relacional, sinó més aviat la competència, i molt especialment Oracle,
empresa que va néixer, justament, amb el nom de Relational Software.
Contingut
Estructuració de les dades
El model relacional permet construir estructures de dades per representar les diferents
informacions del món real que tinguin algun interès.
Les estructures de dades construïdes seguint el model relacional estan formades per conjunts de relacions.
Les relacions poden ser concebudes com a representacions tabulars de les dades.
Tuple
En l’àmbit de les BD, podem definir tuple com una seqüència finita
d’objectes que comprèn les diferents associacions entre cada atribut
de la relació i un valor concret, admissible dins del domini respectiu.
Cal precisar els extrems següents:
- Tota relació ha de tenir un nom que la identifiqui unívocament dins de la base de dades.
- Cada fila està constituïda per un tuple de dades relacionades entre elles, anomenat també registre, que guarda les dades que ens interessa reflectir d’un objecte concret del món real.
- En canvi, cada columna conté, en cada cel·la, dades d’un mateix tipus, i se la pot anomenar atribut o camp.
- Cada cel·la, o intersecció entre fila i columna, pot emmagatzemar un únic valor.
Exemple de relació
La següent taula reflecteix l’estructuració tabular de la relació ALUMNE, que conté les dades
personals corresponents als individus matriculats en un centre docent.
Cada fila conté unes quantes dades relacionades que, en aquest cas, són les que pertanyen a un
mateix alumne.
La relació té un nom (ALUMNE), com cadascuna de les columnes (DNI, Nom, Cognoms i Telefon). Si
aquests noms són prou significatius, permeten copsar de seguida el sentit que tenen els valors
de les dades emmagatzemades en la relació.
Taula Exemple de relació
ALUMNE
-------------------------------------------------
DNI Nom Cognoms Telefon
47126654F Josep Bel Rovira 453641282
51354897S Anna Pacheco Cuscó 723352151
56354981L Xavier Rius Montalvo 726922235
Tota base de dades relacional està formada per un conjunt de relacions.
Aquesta senzilla manera de visualitzar l’estructura de les bases de dades relacionals resulta molt entenedora per a la majoria d’usuaris. Però cal aprofundir en algunes característiques addicionals de les relacions, per talde poder-les distingir clarament dels fitxers tradicionals.
Domini
Pel que fa al model relacional, un domini consisteix en un conjunt finit de valors indivisibles.
Els atributs només poden prendre els valors que estiguin inclosos dins del domini respectiu. Altrament no són valors vàlids, i un SGBD relacional no en pot permetre l’emmagatzematge.
Exemples de dominis
Examinem l’atribut Telefon de la relació ALUMNE. Si el definim de tal manera que només pugui
emmagatzemar nou caràcters (perquè els telèfons sempre consten de nou dígits) de tipus numèric
(ja que les lletres no poden formar part d’un número de telèfon), el domini d’aquest atribut
inclourà totes les combinacions possibles (en concret,10⁹ , que és una magnitud gran, però finita).
Una altra cosa és que molts d’aquests valors no es podran correspondre mai amb valors existents
en el món real (per exemple, difícilment un operador assignarà a un dels seus abonats una cadena
de nou zeros com a identificador telefònic). Per aconseguir-ho, caldria restringir força més el
domini de l’atribut a l’hora de definir-lo.
Centrem-nos ara en l’atribut Cognoms. Contindrà els valors dels dos cognoms dels alumnes que els
tinguin, separats per un espai en blanc. Per tant, aquest camp està definit per tal que pugui
emmagatzemar dos objectes del món real: primer cognom i segon cognom.
Conceptualment, els usuaris podran distingir entre els dos objectes representats, i els programadors
d’aplicacions podran truncar, en cas necessari, el resultat obtingut en fer una consulta del camp
Cognoms. Però tot SGBD relacional considerarà el valor contingut en l’atribut Cognoms de manera
atòmica, sense cap estructuració interna.
Hem de considerar dues tipologies de dominis:
- Dominis predefinits. Són els tipus de dades que admeti cada SGBD, com, per exemple (esmentats de manera genèrica, ja que hi ha moltes especificitats en funció dels diferents sistemes gestors), les cadenes de caràcters, els nombres enters, els nombres decimals, les dades de caire cronològic, etc.
- Dominis definits pels usuaris. Consisteixen en restriccions addicionals aplicades sobre el domini predefinit d’alguns atributs, establertes pels dissenyadors i pels administradors de bases de dades.
Exemple de domini definit per l'usuari
En una relació per emmagatzemar les dades dels aspirants a mosso d’esquadra, es podria establir el
camp IMC, per registrar els índexs de massa corporal respectius.
Doncs bé, es podria restringir el domini d’aquest camp de tal manera que no admetés aspirants amb
valors inferiors a dinou ni superiors a trenta, ja que la normativa no ho permet.
Esquema i extensió
Tota relació consta d’un esquema (també anomenat intensió de la relació) i de la seva extensió.
L’esquema d’una relació consisteix en un nom que la identifica unívocament dins de la
base de dades, i en el conjunt d’atributs que aquella conté.
És molt recomanable, per tal d’evitar confusions en la implementació ulterior, seguir uniformement una notació concreta a l’hora d’expressar els esquemes de les relacions que formen una mateixa base de dades.
A continuació, es detallen les característiques d’un dels sistemes de notació més freqüents:
- Cal escriure el nom de les relacions amb majúscules i preferiblement en singular.
- S’ha d’escriure el nom dels atributs començant amb majúscula i continuant amb minúscules, sempre que no es tracti de sigles, ja que aleshores és més convenient deixar totes les lletres amb majúscules (com ara DNI). Per tal de fer els noms compostos més llegidors, es pot encapçalar cada paraula de les que formen el nom del camp amb una lletra majúscula (per exemple: DataNaixement, TelefonParticular, etc.).
Exemple d'esquema d'una relació
L’esquema de la relació que es mostra en la següent taula, conforme al sistema de notació proposat,
quedaria com segueix:
ALUMNE(DNI, Nom, Cognoms, Telefon)
Cal precisar que l’ordre en què ens mostrin els atributs és indiferent, per definició del model
relacional.
Taula Exemple de relació
ALUMNE
------------------------------------------------
DNI Nom Cognoms Telefon
47126654F Josep Bel Rovira 453641282
51354897S Anna Pacheco Cuscó 723352151
56354981L Xavier Rius Montalvo 726922235
Els atributs d’una relació són únics dins d’aquesta. El seu nom no pot estar repetit dins d’una mateixa relació. Ara bé, diferents relacions sí que poden contenir atributs amb el mateix nom.
D’altra banda, cal dir que els dominis de diferents atributs d’una mateixa relació poden ser idèntics, malgrat que els camps respectius emmagatzemin els valors de diferents propietats de l’objecte (per exemple, seria perfectament lògic que els atributs TelefonFix, TelefonMobil i TelefonFeina, tot i pertànyer a una mateixa relació, tinguessin el mateix domini).
L’extensió d’una relació consisteix en els valors de les dades emmagatzemades en tots els
tuples que aquesta conté.
Exemple d'extensió
Si prenem com a base, una vegada més, la relació amb esquema ALUMNE(DNI, Nom, Cognoms,
Telefon) de la taula 2, la seva extensió seria una llista en què figurarien tots els alumnes
de la base de dades:
Alumne 1: 47126654F, Josep, Bel Rovira, 453641282 Alumne 2: 51354897S, Anna, Pacheco Cuscó,
723352151 Alumne 3: 56354981L, Xavier, Rius Montalvo, 726922235
De vegades, els atributs de les relacions poden no contenir cap valor o, dit d’una altra manera, poden contenir valors nuls.
Exemple de valor nul
Imaginem que s’hi matricula un quart alumne que no té telèfon. Les seves dades en la coneguda
relació amb esquema ALUMNE(DNI, Nom, Cognoms, Telefon) reflectiran aquesta circumstància amb
l’absència de valor en l’atribut Telefon del tuple que li correspongui.
En utilitzar representacions tabulars per visualitzar els valors de les extensions de les
relacions (en el pla teòric, no en implementacions reals amb SGBD), per tal d’indicar que una
cel·la té valor nul s’hi pot incloure el mot NUL (com en la taula anterior), o bé es pot deixar en
blanc, simplement.
Taula Exemple de relació amb valors nuls
ALUMNE
-------------------------------------------
DNI Nom Cognoms Telefon
47126654F Josep Bel Rovira 453641282
51354897S Anna Pacheco Cuscó 723352151
56354981L Xavier Rius Montalvo 726922235
24583215W Mariona Castellví Mur NUL
El grau d’una relació depèn del nombre d’atributs que inclou el seu esquema.
Exemple de grau d'una relació
La relació amb esquema ALUMNE(DNI, Nom, Cognoms, Telefon) de la taula anterior és de grau 4,
perquè té quatre atributs.
La cardinalitat d’una relació ve donada pel nombre de tuples que en formen l’extensió.
Exemple de cardinalitat
Si ens fixem en la taula anterior, la cardinalitat de la relació ALUMNE és 4, perquè la seva
extensió conté quatre tuples corresponents als quatre alumnes que, de moment, hi ha
matriculats.
Claus candidates, clau primària i claus alternatives
Per tal de resultar útil, l’emmagatzematge de la informació ha de permetre la identificació de les dades. En l’àmbit de les bases de dades relacionals, els tuples de les relacions s’identifiquen mitjançant les anomenades superclaus.
Una superclau és un subconjunt dels atributs que formen l’esquema d’una relació tal que
no és possible que hi hagi més d’un tuple en l’extensió respectiva, amb la mateixa combinació
de valors en els atributs que formen part del subconjunt esmentat.
Però una superclau pot contenir atributs innecessaris, que no contribueixen a la identificació inequívoca dels diferents tuples. El que habitualment interessa és treballar amb superclaus mínimes, tals que cap subconjunt propi sigui capaç per sí sol d’identificar els tuples de la relació.
Per definició, cap superclau mínima no pot admetre valors nuls en cap dels seus atributs, perquè si ho fes, no podria garantir la identificació inequívoca dels tuples que continguessin algun valor nul en alguns dels atributs de la superclau mínima en qüestió.
D’altra banda, cal dir que en una mateixa relació pot passar que hi hagi més d’una superclau mínima que permeti distingir els tuples unívocament entre ells.
S’anomenen claus candidates totes les superclaus mínimes d’una relació formades pels atributs
o conjunts d’atributs que permeten identificar els tuples que conté la seva extensió.
Tria de la clau primària
Amb molta freqüència, és l’administrador de la BD qui tria la clau primària
de la relació, d’entre les claus candidates disponibles, tot realitzant, en
el fons, tasques de dissenyador lògic.
Però, a l’hora d’implementar una BD, entre totes les claus candidates de cada relació només se n’ha de triar una.
Quan parlem de clau primària ens referim a la clau que, finalment, el dissenyador lògic
de la base de dades tria per distingir unívocament cada tuple d’una relació de la resta.
Aleshores, les claus candidates no triades com a clau primària resten presents en la relació.
Quan una relació ja té establerta una clau primària, la resta de claus presents en aquella,
i que també podrien servir per identificar els diferents tuples de l’extensió respectiva,
es coneixen com a claus alternatives.
Una forma de diferenciar els atributs que formen la clau primària de les relacions, dels altres atributs de l’esquema respectiu, és posar-los subratllats. Per aquest motiu, normalment es col·loquen junts i abans que la resta d’atributs, dins de l’esquema. Però només es tracta d’una qüestió d’elegància, ja que el model relacional no es basa ni en l’ordre dels atributs de l’esquema, ni tampoc en l’ordre dels tuples de l’extensió de la relació.
Exemples de claus candidates, primària i alternatives
Observant la taula.4, podem imaginar que la relació ALUMNE té uns quants atributs més, de
manera que el seu esquema queda com segueix:
ALUMNE(DNI, NumSS, NumMatricula, Nom, Cognoms, Telefon)
Veurem fàcilment com els atributs DNI, NumSS (número de la Seguretat Social) i NumMatricula,
en ser personals i irrepetibles, ens podrien servir per identificar unívocament els alumnes.
Per tant, serien claus candidates.
Aleshores, el dissenyador de BD s’haurà de decidir per una clau candidata com a clau primària.
Si, per exemple, tria DNI com a clau primària, les antigues claus candidates restants es
passaran a considerar claus alternatives.
En aquest cas, doncs, l’esquema resultant haurà de reflectir quina és la clau primària de la
relació, tot subratllant l’atribut DNI:
ALUMNE(DNI, NumSS, NumMatricula, Nom, Cognoms, Telefon)
Taula Exemple de relació amb valors nuls
ALUMNE
--------------------------------------------------
DNI Nom Cognoms Telefon
47126654F Josep Bel Rovira 453641282
51354897S Anna Pacheco Cuscó 723352151
56354981L Xavier Rius Montalvo 726922235
24583215W Mariona Castellví Mur NUL
Si no es disposa d’un atribut que sigui capaç d’identificar els tuples de la relació per si sol, cal buscar un subconjunt d’atributs, tals que la combinació dels valors que adoptin no es pugui repetir. Si aquesta possibilitat no existeix, cal afegir a la relació un atribut addicional que faci d’identificador.
Per definició, el model relacional no admet tuples repetits, és a dir, no permet l’existència
de tuples en una mateixa relació que tinguin els mateixos valors en cadascun dels atributs.
Ara bé, les implementacions concretes dels diferents SGBD sí que permeten aquesta possibilitat, sempre que no s’estableixi cap clau primària en la relació amb tuples repetits.
Aquesta permissivitat de vegades permet solucionar certes eventualitats, però no hauria de ser la manera habitual de treballar amb BD relacionals.
Claus foranes
Qualsevol BD relacional, per petita que sigui, conté normalment més d’una relació. Per tal de reflectir correctament els vincles existents entre alguns objectes del món real, cal que els tuples de les diferents relacions d’una base de dades es puguin interrelacionar.
De vegades, fins i tot pot ser necessari relacionar els tuples d’una relació amb altres tuples de la mateixa relació.
El mecanisme que ofereixen les BD relacionals per interrelacionar les relacions que contenen es fonamenta en les anomenades claus foranes.
Una clau forana està constituïda per un atribut, o per un conjunt d’atributs, de l’esquema
d’una relació, que serveix per relacionar els seus tuples amb els tuples d’una altra relació
de la base de dades (o amb els tuples d’ella mateixa, en alguns casos).
Per tal d’aconseguir connectar els tuples d’una relació amb els d’una altra (o amb les seves pròpies), la clau forana utilitzada ha de referenciar la clau primària de la relació amb la qual es vol relacionar.
Les diferents combinacions de valors dels atributs de tota clau forana han d’existir en la clau primària a què fan referència, o bé han de ser valors nuls. Altrament, les referències serien errònies i, per tant, les dades serien incorrectes.
Cal parar atenció en les característiques següents de les claus foranes:
- Tota clau forana ha de tenir el mateix nombre d’atributs que la clau primària a la qual fa referència.
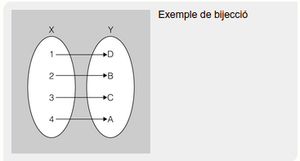
- Entre els atributs de l’esquema d’una clau forana i els de la clau primària respectiva s’ha de poder establir una correspondència (concretament, una bijecció).
- Els dominis dels atributs de tota clau forana han de coincidir amb els dominis dels atributs de la clau primària respectiva (o, com a mínim, cal que siguin compatibles dins d’un cert rang).
Una relació pot contenir més d’una clau forana, o bé no contenir-ne cap. I, en sentit invers, la clau primària d’una relació pot estar referenciada per una o més claus forànies, o bé pot no estar referenciada per cap.
Finalment, cal dir que es pot donar el cas que un mateix atribut formi part tant de la clau primària de la relació com d’alguna de les seves claus foranes.
Exemples de claus foranes
La relació ALUMNE, tal com es mostra en la taula.5, incorpora dues claus foranes.
Una d’elles, CodiAula, fa referència a la clau primària de la relació AULA (formada
per l’atribut Codi), exposada en la taula.6, per tal d’indicar quina aula correspon
a cada alumne.
En canvi, DNIDelegat fa referència a la clau primària de la mateixa relació (formada
per l’atribut DNI), i serveix per indicar quin és el delegat que representa cada alumne.
Fixem-nos que l’alumna Mariona Castellví encara no té assignat ni delegat ni aula i, per
aquest motiu, el tuple que la representa conté, de moment, valors nuls en els atributs de
les dues claus foranes.
Taula Exemple de relació amb claus foranes
ALUMNE
---------------------------------------------------------------------------------
DNI Nom Cognoms Telefon DNIDelegat CodiAula
47126654F Josep Bel Rovira 453641282 47126654F 102
51354897S Anna Pacheco Cuscó 723352151 51354897S 201
56354981L Xavier Rius Montalvo 726922235 51354897S 201
24583215W Mariona Castellví Mur NUL NUL NUL
Taula Exemple de relació amb clau primària referenciada
AULA
---------------------
Codi Capacitat
101 40
102 36
201 30
La notació més habitual per designar les claus foranes de les relacions consisteix a afegir aquesta circumstància a continuació del seu esquema, incloent-hi entre dues claus el conjunt d’atributs que formen la clau forana de què es tracti, precedit de l’adverbi ON, i seguit de la forma verbal REFERENCIA i de la relació a què fa referència. Si hi ha més d’una clau forana, se separen per comes i l’última ha d’anar precedida de la conjunció I.
Exemple de notació per designar claus foranes
Les dues relacions que es mostren en les taules 5 i 6 s’expressaran de la manera següent:
ALUMNE(DNI, Nom, Cognoms, Telefon, DNIDelegat, CodiAula) ON {DNIDelegat} REFERENCIA ALUMNE
i {CodiAula} REFERENCIA AULA
AULA(Codi, Capacitat)
Operacions amb relacions
El model relacional permet realitzar una sèrie d’operacions amb les dades emmagatzemades en les BD, les quals tenen diferents finalitats:
- Actualització. Aquestes operacions realitzen canvis en els tuples que queden reflectits en les relacions que contenen les BD. Poden ser de tres tipus:
- Inserció. Consisteix a afegir un o més tuples nous a una relació determinada.
- Esborrat. Consisteix a eliminar un o més tuples nous d’una relació determinada.
- Modificació. Consisteix a canviar el valor d’un o més atributs d’un o més tuples d’una relació determinada.
- Consulta. Aquestes operacions només fan possible l’obtenció parametritzada de dades, sense que es vegin alterades les emmagatzemades en la BD.
La realització d’aquestes operacions comporta el coneixement previ de l’estructura formada per les relacions que sigui necessari utilitzar, és a dir, els esquemes de les relacions i les interrelacions entre elles, mitjançant les claus foranes.
Exemples d'operacions
Si prenem en consideració la relació ALUMNE que mostra la taula.7, un exemple d’inserció
consistirà a afegir un nou alumne, com ara el següent:
<65618724G, Lídia, Bofarull Mora, 564628231, 47126654F, 102>
Un exemple d’esborrament seria eliminar el tuple que conté les dades d’un alumne donat
d’alta, com ara el següent:
<56354981L, Xavier, Rius Montalvo, 726922235, 51354897S, 201>
Un exemple de modificació seria, per exemple, canviar el número de telèfon de Josep Bel
Rovira que consta en la BD (453641282) per un altre (546022547), per tal de reflectir
correctament la realitat, de manera actualitzada, o bé assignar-ne un de nou a algú que
abans no en tenia, com la Mariona Castellví Mur, introduint 875261473 en lloc de l’anterior
valor nul.
I, com a exemple de consulta, ens podria interessar obtenir una llista, ordenada
alfabèticament pels cognoms, de tots els alumnes que són delegats d’aula i que, per tant,
tenen valors coincidents en l’atribut DNI i en l’atribut DNIDelegat. En aquest cas, el
resultat seria el següent:
___________________________________________________________________________________
<47126654F, Josep, Bel Rovira, 546022547, 47126654F, 102>
<51354897S, Anna, Pacheco Cuscó, 723352151, 51354897S, 201>
___________________________________________________________________________________
Taula Exemple de relació amb claus foranes
ALUMNE
----------------------------------------------------------------------------
DNI Nom Cognoms Telefon DNIDelegat CodiAula
47126654F Josep Bel Rovira 453641282 47126654F 102
51354897S Anna Pacheco Cuscó 723352151 51354897S 201
56354981L Xavier Rius Montalvo 726922235 51354897S 201
24583215W Mariona Castellví Mur NUL NUL NUL
Regles d'integritat
Els valors que emmagatzemen les BD han de reflectir en tot moment, de manera correcta, la porció de la realitat que volem modelitzar.
Anomenem integritat la propietat de les dades que consisteix a representar correctament
les situacions del món real que modelitzen.
Per tal que les dades siguin íntegres, cal garantir que siguin correctes, i també que estiguin senceres.
En atenció a l’objectiu esmentat, doncs, les dades han de complir certes condicions, que podem agrupar en dues tipologies diferents:
- Restriccions d’integritat de l’usuari. Són condicions específiques de cada BD. Els SGBD han de permetre als administradors establir certes restriccions aplicables a casos concrets, i han de garantir que es respectin durant l’explotació habitual del sistema.
- Regles d’integritat del model. Són condicions de caire general que han de complir totes les BD que segueixin el model relacional. No cal definir-les en implementar cada BD, perquè es consideren preestablertes.
Exemple de restricció d'integritat de l'usuari
En donar d’alta un nou alumne de la relació ALUMNE, que es mostra en la taula 8, podríem
exigir al sistema que el validés, mitjançant l’algorisme corresponent, si la lletra introduïda
del NIF es correspon amb les xifres introduïdes prèviament, i que denegués la inserció en cas
contrari, per tal de no emmagatzemar una situació en principi no admissible en el món real.
Exemple de regla d'integritat del model
Com que la relació ALUMNE, que es mostra en la taula.8, té definit l’atribut DNI com a clau
primària, el sistema validarà automàticament que no s’introdueixi més d’un alumne amb el mateix
carnet d’identitat, ja que aleshores la clau primària no compliria el seu objectiu de garantir
la identificació inequívoca de cada tuple, diferenciant-lo de la resta.
Taula Exemple de relació amb claus foranes
ALUMNE
-----------------------------------------------------------------------------
DNI Nom Cognoms Telefon DNIDelegat CodiAula
47126654F Josep Bel Rovira 453641282 47126654F 102
51354897S Anna Pacheco Cuscó 723352151 51354897S 201
56354981L Xavier Rius Montalvo 726922235 51354897S 201
24583215W Mariona Castellví Mur NUL NUL NUL
Unicitat de la clau primària
El valor d’una clau primària, globalment considerada, no pot estar repetit en més d’un tuple de la mateixa relació, ja que aleshores la clau primària no estaria en condicions d’assegurar la identificació inequívoca dels diferents tuples.
En cap moment, no hi pot haver dos o més tuples amb la mateixa combinació de valors
en el conjunt dels atributs que formen la clau primària d’una relació.
Els SGBD relacionals han de garantir la regla d’unicitat de la clau primària en totes les insercions de nous tuples, i també en totes les modificacions que afectin el valor d’algun dels atributs que formin part de la clau primària.
Exemple d'unicitat de la clau primària
En la relació AULA, que es mostra en la taula.9, no s’hauria de poder inserir un nou tuple
amb els valors <102, 40>, perquè la clau primària ja emmagatzema el valor 102, corresponent
a un altre tuple.
Si volem donar d’alta una altra aula al primer pis de l’edifici amb capacitat per a quaranta
alumnes, haurem d’utilitzar com a clau primària un altre valor no present en l’atribut Codi,
i resultarà, per exemple, <103, 40>.
Tampoc no hauria de ser possible modificar la clau del tuple <101, 40> i assignar-hi el valor
102, perquè aquest valor ja el té assignat la clau primària d’un altre tuple.
Taula Exemple de relació amb clau primària referenciada
AULA
---------------------
Codi Capacitat
101 40
102 36
201 30
Entitat de la clau primària
Les claus primàries serveixen per diferenciar cada tuple d’una relació de la resta de tuples de la mateixa relació. Per garantir la consecució d’aquesta finalitat, cal que els atributs que formen part d’una clau primària no puguin tenir valor nul ja que, si s’admetés aquesta possibilitat, els tuples amb valors nuls en la clau primària no es podrien distingir d’alguns altres.
Cap atribut que formi part d’una clau primària no pot contenir mai valors nuls en cap tuple.
Els SGBD relacionals han de garantir la regla d’entitat de la clau primària en totes les insercions de nous tuples, com també en totes les modificacions que afectin el valor d’algun dels atributs que formin part de la clau primària.
Exemple d'entitat de la clau primària
En la relació AULA, que es mostra en la taula.10, no s’hauria de poder inserir un nou tuple
amb els valors <NUL, 26>, perquè la clau primària, per definició, no pot contenir valors nuls.
Si volem donar d’alta una altra aula amb capacitat per a vint-i-sis alumnes, haurem d’utilitzar
com a clau primària un altre valor no nul, i resultarà, per exemple, <202, 26>.
Tampoc no hauria de ser possible, per la mateixa raó que hem exposat més amunt, modificar la
clau del tuple <101, 40> i assignar-hi el valor nul.
Taula Exemple de relació amb clau primària referenciada
AULA
---------------------
Codi Capacitat
101 40
102 36
201 30
Integritat referencial
El model relacional no admet, per definició, que la combinació de valors dels atributs que formen una clau forana no sigui present en la clau primària corresponent, ja que això implicaria una connexió incorrecta.
La integritat referencial implica que, per a qualsevol tuple, la combinació de valors que
adopta el conjunt dels atributs que formen la clau forana de la relació o bé ha de ser present
en la clau primària a la qual fa referència, o bé ha d’estar constituïda exclusivament per valors
nuls (si els atributs implicats admeten aquesta possibilitat, i així s’ha estipulat en definir-ne
les propietats).
Els SGBD relacionals hauran de fer les comprovacions pertinents, de manera automàtica, per tal de garantir la integritat referencial, quan es produeixin dos tipus d’operacions amb relacions que tinguin claus foranes:
- Insercions de nous tuples.
- Modificacions que afectin atributs que formin part de qualsevol clau forana.
D’altra banda, els SGBD relacionals també hauran de validar la correcció d’uns altres dos tipus d’operacions amb relacions que tinguin la clau primària referenciada des d’alguna clau forana:
- Esborraments de tuples.
- Modificacions que afectin atributs que formin part de la clau primària.
Per tal de garantir la integritat referencial en aquests dos últims tipus d’operació, es pot seguir alguna de les tres polítiques següents: restricció, actualització en cascada i anul·lació.
Exemple de violació de la integritat referencial
Continuem especulant amb les relacions ALUMNE i AULA (reflectides en la taula.11 i taula.12
respectivament).
El tuple que conté les dades de Mariona Castellví Mur té un valor nul en l’atribut que forma
la clau forana que fa referència a la relació AULA.
Si el volguéssim actualitzar amb el valor 316, per exemple, el sistema no ens ho hauria de
deixar fer, perquè aquest valor no és present en la clau primària de cap tuple de la relació
AULA i, per tant, aquesta operació contravindria la regla d’integritat referencial.
Taula Relació amb claus foranes
ALUMNE
-----------------------------------------------------------------------------
DNI Nom Cognoms Telefon DNIDelegat CodiAula
47126654F Josep Bel Rovira 453641282 47126654F 102
51354897S Anna Pacheco Cuscó 723352151 51354897S 201
56354981L Xavier Rius Montalvo 726922235 51354897S 201
24583215W Mariona Castellví Mur NUL NUL NUL
Taula Relació amb clau primària referenciada
AULA
-----------------
Codi Capacitat
101 40
102 36
201 30
Política de restricció
La política de restricció consisteix a prohibir l’operació d’actualització de què es tracti:
- En cas d’esborrament, no permetrà eliminar un tuple si la seva clau primària està referenciada des d’alguna clau forana.
- En cas de modificació, no permetrà alterar el valor de cap dels atributs que formen la clau primària d’un tuple, si aquesta està referenciada des d’alguna clau forana.
Exemples de restriccions
Considerem una vegada més les relacions ALUMNE i AULA que es mostren en la taula.13 i
taula.14 respectivament.
Aplicant la restricció tant en cas d’esborrament com de modificació, aquestes operacions no
seran possibles amb l’aula 102 de la relació AULA perquè hi ha alumnes matriculats que han
d’assistir a classe dins d’aquest espai i, per tant, la referencien des de la clau forana
dels tuples que els representen. Sí seria possible, en canvi, esborrar l’aula 101, perquè no
està referenciada des de la relació ALUMNE.
Taula Relació amb claus foranes
ALUMNE
------------------------------------------------------------------------------
DNI Nom Cognoms Telefon DNIDelegat CodiAula
47126654F Josep Bel Rovira 453641282 47126654F 102
51354897S Anna Pacheco Cuscó 723352151 51354897S 201
56354981L Xavier Rius Montalvo 726922235 51354897S 201
24583215W Mariona Castellví Mur NUL NUL NUL
Taula Relació amb clau primària referenciada
AULA
-------------------
Codi Capacitat
101 40
102 36
201 30
Actualització en cascada
La política d’actualització en cascada consisteix a permetre l’operació d’actualització de què es tracti sobre un tuple determinat, però disposant al mateix temps una sèrie d’operacions compensatòries que propaguin en cascada les actualitzacions necessàries per tal que es mantingui la integritat referencial dels tuples que referencien, des dels atributs que en formen la clau forana, el tuple objecte d’actualització:
- En cas d’esborrament, s’eliminaran tots els tuples que facin referència al tuple esborrat.
- En cas de modificació, els valors dels atributs que formin part de la clau forana dels tuples que facin referència al tuple modificat s’alteraran per tal de continuar coincidint amb els nous valors de la clau primària del tuple al qual fan referència.
Exemples d'actualització en cascada
Tornem a prendre com a punt de partida dels exemples les relacions ALUMNE i AULA que es
mostren en la taula.15 i taula.16 respectivament.
Si apliquem l’actualització en cascada tot esborrant el tuple <201, 30> de la relació AULA,
també s’esborraran els dos tuples de la relació ALUMNE que hi fan referència des de la clau
forana respectiva (CodiAula).
En canvi, si apliquem l’actualització en cascada tot modificant el tuple <201, 30> de la
relació AULA, canviant el valor de la seva clau primària per un altre, com ara 203, els dos
tuples de la relació ALUMNE que hi fan referència actualitzaran en cascada el valor de
l’atribut CodiAula de 201 a 203, per tal de mantenir la connexió correcta entre els tuples
d’ambdues relacions.
Taula Relació amb claus foranes
ALUMNE
----------------------------------------------------------------------------
DNI Nom Cognoms Telefon DNIDelegat CodiAula
47126654F Josep Bel Rovira 453641282 47126654F 102
51354897S Anna Pacheco Cuscó 723352151 51354897S 201
56354981L Xavier Rius Montalvo 726922235 51354897S 201
24583215W Mariona Castellví Mur NUL NUL NUL
Taula Relació amb clau primària referenciada
AULA
----------------
Codi Capacitat
101 40
102 36
201 30
Política d'anul·lació
La política d’anul·lació consisteix a permetre l’operació d’actualització de què es tracti en un tuple determinat, però disposant al mateix temps una sèrie d’operacions compensatòries que posin valors nuls en tots els atributs que formin part de les claus foranes dels tuples que facin referència al tuple objecte d’actualització:
- En cas d’esborrament, els atributs de la clau forana dels tuples que facin referència al tuple esborrat passaran a tenir valor nul, i no indicaran cap tipus de connexió.
- En cas de modificació, els atributs de la clau forana dels tuples que facin referència al tuple modificat passaran a tenir valor nul, i no indicaran cap tipus de connexió.
La política d’anul·lació només es pot aplicar si els atributs de les claus foranes implicades admeten els valors nuls.
Exemple d'anul·lació
Prenem una vegada més com a punt de partida dels exemples les relacions ALUMNE i AULA
que es mostren en la taula.17 i taula.18 respectivament.
Aplicant la política d’anul·lació, tant si esborrem el tuple <102, 36> de la relació AULA,
com si només canviem el valor de l’atribut de la seva clau primària (Codi) per un altre
(com, per exemple, 105), el tuple de la relació ALUMNE que hi fa referència actualitzarà el
valor de l’atribut CodiAula de 102 a valor nul, per tal d’evitar una connexió incorrecta entre
els tuples d’ambdues relacions, i aleshores resultarà el tuple següent:
<47126654F, Josep, Bel Rovira, 453641282, 47126654F, NUL>
Taula Relació amb claus foranes
ALUMNE
----------------------------------------------------------------------------
DNI Nom Cognoms Telefon DNIDelegat CodiAula
47126654F Josep Bel Rovira 453641282 47126654F 102
51354897S Anna Pacheco Cuscó 723352151 51354897S 201
56354981L Xavier Rius Montalvo 726922235 51354897S 201
24583215W Mariona Castellví Mur NUL NUL NUL
Taula Relació amb clau primària referenciada
AULA
----------------
Codi Capacitat
101 40
102 36
201 30
Selecció de la política que s'ha de seguir
Serà el dissenyador de cada BD qui escollirà la política més adequada que s’ha de seguir en cada cas concret. Com a orientació, convé saber que les opcions més freqüents, sempre que no calgui fer consideracions addicionals, són les següents:
- En cas d’esborrament, normalment s’opta per la restricció.
- En cas de modificació, el més habitual és optar per l’actualització en cascada.
La política d’anul·lació és molt menys freqüent, i es posa en pràctica quan es volen conservar certes dades, encara que hagin perdut la connexió que tenien abans, de vegades amb l’esperança que la puguin recuperar més endavant.
Integritat del domini
La regla d’integritat del domini implica que tots els valors no nuls que contenen els atributs de les relacions de qualsevol BD han de pertànyer als respectius dominis declarats per als atributs en qüestió.
Aquesta condició és aplicable tant pel que fa als dominis predefinits, com també pel que fa als dominis definits per l’usuari.
La regla d’integritat del domini també comporta que els operadors que és possible aplicar sobre els valors depenen dels dominis dels respectius atributs que els emmagatzemen.
Exemples d'integritat de domini
Fixem-nos, per últim cop, en la relació AULA que es mostra en la taula.19.
Taula Exemple de relació amb clau primària referenciada
AULA
Codi Capacitat
101 40
102 36
201 30
Si en la relació amb esquema AULA(Codi, Capacitat) definim el domini de l’atribut Codi com el dels nombres enters de 0 fins a 999, aleshores no podrem inserir, per exemple, un valor en l’atribut que forma la clau primària que no pertanyi al seu domini, com ara INF, o LAB.
Tampoc no podrem aplicar determinats operadors per comparar valors de la clau primària amb valors que no pertanyin al seu domini. Així, no podrem consultar les característiques d’una aula amb Codi=‘INF’, ja que ‘INF’ és una cadena de caràcters.
Traducció del model Entitat-Relació al model relacional
Model Entitat Relació o model ER
El model ER és un model de dades que té com a resultat un diagrama
ER o diagrama Chen on gràficament es poden identificar els principals
elements de dades, les seves característiques més importants i les
interrelacions entre els mateixos.
Una vegada conegudes les característiques d’un model de bases de dades relacional, caldrà partir del model conceptual general (del model Entitat-Relació) i fer un estudi del disseny lògic de bases de dades en aquest àmbit, el relacional.
En tots els exemples, pressuposarem que prèviament ha tingut lloc una fase de disseny conceptual de la qual ha resultat un model Entitat-Relació (o model ER) recollit en els diagrames Chen de què es tracti en cada cas.
Fases del disseny de BD
Les fases del disseny de BD són:
1. Disseny conceptual
2. Disseny lògic
3. Disseny físic
Abans d’implementar pròpiament la BD dins de l’entorn ofert pel SGBD utilitzat, cal transformar aquests diagrames en estructures de dades relacionals.
El model ER es basa en les entitats i en les interrelacions existents entre aquestes. Podem avançar uns quants aspectes generals sobre com s’han de traduir aquests elements al model relacional:
- Les entitats sempre donen lloc a relacions, siguin del tipus que siguin (a excepció de les entitats auxiliars de tipus DATA).
- Les interrelacions binàries de connectivitat 1-1 o 1-N originen claus foranes en relacions ja existents.
- Les interrelacions binàries de connectivitat M-N i totes les n-àries d’ordre superior a 2 sempre es transformen en noves relacions.
És convenient seguir un cert ordre a l’hora de dissenyar lògicament una base de dades. Una bona pràctica pot consistir a procedir de la manera següent:
- 1. En primer lloc, cal transformar les entitats del diagrama amb el qual treballem en relacions.
- 2. Després s’ha de continuar transformant en relacions les entitats que presenten algun tipus d’especificitat (és a dir, les febles, les associatives, o les derivades d’un procés de generalització o especialització).
- 3. A continuació, s’han d’afegir a les anteriors relacions els atributs necessaris per formar les claus foranes derivades de les interrelacions binàries amb connectivitat 1-1 i 1-N presents en el diagrama ER.
- 4. I, finalment, ja pot començar la transformació de les interrelacions binàries amb connectivitat M-N i de les interrelacions n-àries.
Cap SGBD no pot resoldre una referència a una taula que encara no ha estat creada.
D’aquesta manera evitarem que hi hagi claus foranes que facin referència a relacions que encara no s’han descrit. Això fa més llegidor el model relacional obtingut, certament, però també estalvia la feina d’haver d’ordenar les relacions a l’hora d’escriure (típicament en llenguatge SQL) i les instruccions pertinents per tal que el SGBD utilitzat creï les taules de la base de dades.
Les tècniques necessàries per realitzar correctament el disseny lògic de bases de dades, segons el tipus de conceptualització de què es tracti en cada cas.
Entitats
Cada entitat del model ER es transforma en una relació del model relacional:
- Els atributs de l’entitat originària seran els atributs de la relació resultant.
- La clau primària de l’entitat originària serà la clau primària de la relació resultant.
- Quan una entitat intervé en alguna interrelació binària 1-1 o 1-N, pot ser necessari afegir ulteriorment nous atributs, per tal que actuïn com a claus foranes de la relació.
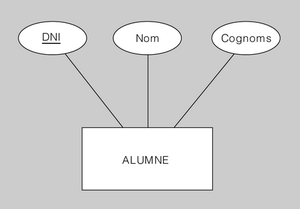
Exemple de transformació d'entitat
El diagrama ER de la figura.1 es tradueix al model relacional de la manera següent:
ALUMNE(DNI, Nom, Cognoms)
---
Interrelacions
Un cop transformades totes les entitats en relacions, cal traduir les interrelacions en què aquelles participen.
1. Binàries. Per traduir les interrelacions binàries cal tenir en compte la seva connectivitat, així com també les dependències d’existència.
a. Connectivitat 1-1 i dependències d’existència. Cal afegir a qualsevol de les dues relacions una clau forana que faci referència a l’altra relació.
Però si una de les dues entitats és opcional en la relació, aleshores és ella qui ha d’acollir la clau forana, per tal d’evitar, en cas contrari, l’emmagatzematge de valors nuls en aquesta, i estalviar-se així espai d’emmagatzematge.
Dependències d'existència
De vegades, una entitat instància només té sentit si hi ha com a mínim una
altra entitat instància que hi està associada mitjançant una interrelació
binària determinada. En aquests casos, es diu de la darrera entitat que és
una entitat obligatòria en la interrelació. Altrament, es diu que es tracta
d’una entitat opcional en la interrelació.
Els atributs de la interrelació (si n’hi ha) acompanyen la clau forana.
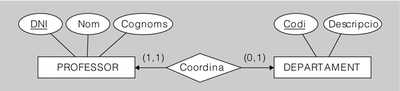
Exemple de transformació d'interrelació binària amb connectivitat 1-1
El diagrama ER de la figura.2 representa una interrelació binària amb connectivitat 1-1.
Per tant, en principi hi hauria dues possibilitats de transformació, segons si es col·loca
la clau forana en l’entitat PROFESSOR o en l’entitat DEPARTAMENT:
DEPARTAMENT(Codi, Descripcio)
PROFESSOR(DNI, Nom, Cognoms, CodiDepartament) ON {CodiDepartament} REFERENCIA DEPARTAMENT i
CodiDepartament ADMET VALORS NULS
O bé:
PROFESSOR(DNI, Nom, Cognoms)
DEPARTAMENT(Codi, Descripcio, DNIProfessor) ON {DNIProfessor} REFERENCIA PROFESSOR
Ara bé, l’entitat DEPARTAMENT és opcional en la interrelació Coordina. Això vol dir que hi
pot haver professors que no coordinin cap departament. Per tant, l’opció més correcta
consisteix a afegir la clau forana a la relació DEPARTAMENT, ja que si s’afegís a la relació
PROFESSOR hauria de prendre el valor nul en molts casos, i ocuparia un espai d’emmagatzematge
innecessari.
b. Connectivitat 1-N. En aquests casos cal afegir una clau forana a la relació que resulta de traduir l’entitat ubicada al costat N de la interrelació, que faci referència a l’altra relació.
Si es col·loqués la clau forana en l’altra relació, l’atribut que la forma hauria de ser multivalent per tal de poder representar totes les connexions possibles, i això no està permès dins del model relacional.
Els atributs de la interrelació (si n’hi ha) acompanyen la clau forana.
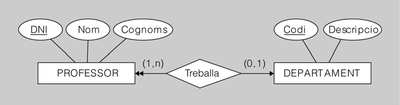
Exemple de transformació d'interrelació binària amb connectivitat 1-N
El diagrama ER de la figura.3 representa una interrelació binària amb connectivitat 1-N.
Per tant, la clau forana s’haurà d’afegir necessàriament a l’entitat derivada de l’entitat
del costat N, i resulta el model següent:
DEPARTAMENT(Codi, Descripcio)
----
PROFESSOR(DNI, Nom, Cognoms, CodiDepartament) ON {CodiDepartament} REFERENCIA DEPARTAMENT i
---
CodiDepartament ADMET VALORS NULS
L’entitat del costat 1 (DEPARTAMENT) és opcional en la interrelació Treballa. Això implica
que l’entitat PROFESSOR admetrà valors nuls en la seva clau forana que fa referència a
DEPARTAMENT, ja que hi podrà haver professors no assignats a cap departament. Però, al
contrari del que passava amb les interrelacions 1-1, aquí no es podran evitar aquests valors
nuls, ja que la clau forana ha d’anar necessàriament a l’entitat que resulta de traduir al
model relacional l’entitat ubicada al costat N de la interrelació.
c. Connectivitat M-N. Cada interrelació M-N es transforma en una nova relació amb les característiques següents:
- La seva clau primària estarà formada pels atributs de les claus primàries de les dues entitats interrelacionades.
- Els atributs de la interrelació (si n’hi ha) es convertiran en atributs de la nova relació.
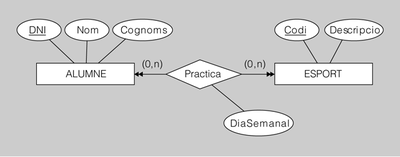
Exemple de transformació d'interrelació binària amb connectivitat M-N
El diagrama ER de la figura.4 es tradueix al model relacional de la manera següent:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripcio)
----
PRACTICA(DNIAlumne, CodiEsport, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE i {CodiEsport}
---------------------
REFERENCIA ESPORT
2. Ternàries. Tota interrelació ternària es transforma en una nova relació, que tindrà per atributs els de les claus primàries de les tres entitats interrelacionades, més els atributs propis de la interrelació, si en té.
La composició de clau primària de la nova relació depèn de la connectivitat de la interrelació ternària originària.
a. Connectivitat M-N-P. En aquest cas, la clau primària està formada per tots els atributs que formen les claus primàries de les tres entitats interrelacionades (si no fos així, la clau primària hauria de repetir algunes combinacions dels seus valors per tal de modelitzar totes les possibilitats, però aquesta possibilitat no està permesa dins del model relacional).
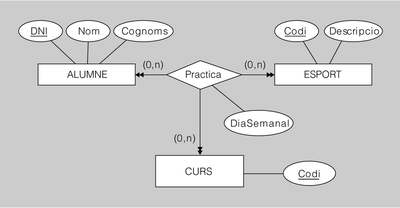
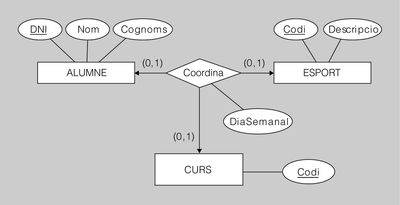
Exemple de transformació d'interrelació ternària amb connectivitat M-N-P
El diagrama ER de la figura.5 es tradueix al model relacional de la manera següent:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripcio)
----
CURS(Codi)
----
PRACTICA(DNIAlumne, CodiEsport, CodiCurs, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE
-------------------------------
{CodiEsport} REFERENCIA ESPORT i {CodiCurs} REFERENCIA CURS
b. Connectivitat 1-M-N. La clau primària està composta per tots els atributs que formen les claus primàries de les dues entitats que són a tots dos costats de la interrelació etiquetats amb una N (o amb el que és equivalent, una fletxa de punta doble).
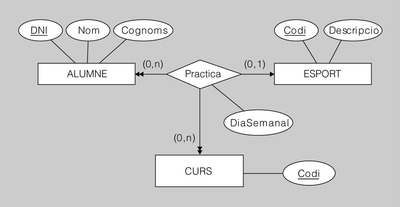
Exemple de transformació d'interrelació ternària amb connectivitat 1-M-N
El diagrama ER de la figura.6 es tradueix al model relacional de la manera següent:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripció)
----
CURS(Codi)
----
PRACTICA(DNIAlumne, CodiCurs, CodiEsport, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE
-------------------
{CodiEsport} REFERENCIA ESPORT, I {CodiCurs} REFERENCIA CURS
Fixem-nos que, en aquest cas, un alumne només pot practicar un esport en cada curs acadèmic
i, per tant, no cal incorporar la clau de l’entitat ESPORT a la clau de la relació PRACTICA.
c. Connectivitat 1-1-N. En aquests casos, la clau primària està composta pels atributs que formen la clau primària de l’entitat del costat N de la interrelació, més els atributs que formen la clau primària de qualsevol de les altres dues entitats connectades amb cardinalitat 1.
Així, doncs, tota nova relació derivada d’una interrelació ternària amb connectivitat 1-1-N disposarà de dues claus candidates. L’elecció d’una d’aquestes com a clau primària de la nova relació quedarà al criteri del dissenyador lògic de BD.
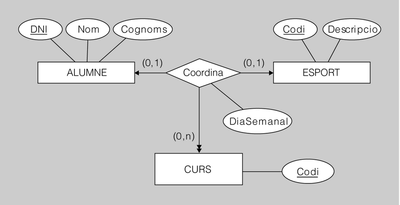
Exemple de transformació d'interrelació ternària amb connectivitat 1-1-N
El diagrama ER de la figura.7 es pot traduir al model relacional de dues maneres:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripció)
----
CURS(Codi)
----
COORDINACIO(CodiCurs, DNIAlumne, CodiEsport, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE
-------------------
{CodiEsport} REFERENCIA ESPORT i {CodiCurs} REFERENCIA CURS
O bé:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripció)
----
CURS(Codi)
----
COORDINACIO(CodiCurs, CodiEsport, DNIAlumne, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE
--------------------
{CodiEsport} REFERENCIA ESPORT i {CodiCurs} REFERENCIA CURS
Es pot veure que hem modificat el nom de la relació derivada de la interrelació per tal
de convertir el verb originari en un substantiu, que normalment és més adequat per designar
relacions.
d. Connectivitat 1-1-1. En aquests casos, la clau primària està composta pels atributs que formen la clau primària de dues entitats qualssevol, ja que totes tres estan connectades amb cardinalitat 1.
Així, doncs, tota nova relació derivada d’una interrelació ternària amb connectivitat 1-1-1 disposarà de tres claus candidates. L’elecció d’una d’aquestes com a clau primària de la nova relació quedarà al criteri del dissenyador lògic de BD.
Exemple de transformació d'interrelació ternària amb connectivitat 1-1-1
El diagrama ER de la figura.8 es pot traduir al model relacional de tres maneres:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripció)
----
CURS(Codi)
----
COORDINACIO(CodiCurs, DNIAlumne, CodiEsport, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE
-------------------
{CodiEsport} REFERENCIA ESPORT i {CodiCurs} REFERENCIA CURS
O bé:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripció)
----
CURS(Codi)
----
COORDINACIO(CodiCurs, CodiEsport, DNIAlumne, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE
--------------------
{CodiEsport} REFERENCIA ESPORT i {CodiCurs} REFERENCIA CURS
O bé:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripció)
----
CURS(Codi)
----
COORDINACIO(CodiEsport, DNIAlumne, CodiCurs, DiaSemanal) ON {DNIAlumne} REFERENCIA ALUMNE
---------------------
{CodiEsport} REFERENCIA ESPORT i {CodiCurs} REFERENCIA CURS
Fixem-nos que hem canviat el significat del diagrama respecte al que hem representat en
la figura.7: ara un alumne només pot coordinar la pràctica d’un esport durant un sol curs
acadèmic, al llarg dels seus estudis, per tal d’afavorir la rotació en els càrrecs de
coordinació del centre.
3. n-àries. Cada interrelació n-ària es transforma en una nova relació, que té com a atributs les claus primàries de totes les entitats relacionades, més els atributs propis de la interrelació originària, si en té.
La composició de la clau primària de la nova relació depèn de la connectivitat de la interrelació n-ària.
a. Connectivitat de totes les entitats amb cardinalitat N. La clau primària està formada per tots els atributs que formen les claus primàries de totes les entitats interrelacionades (n).
Cal seguir el mateix mecanisme que amb les interrelacions ternàries amb connectivitat M-N-P.
b. Connectivitat d’una o més entitats amb cardinalitat 1. La clau primària està formada per tots els atributs que formen les claus primàries de totes les entitats interrelacionades excepte una (n-1). L’entitat que no incorpora la seva clau primària a la de la nova relació ha d’estar forçosament connectada amb un 1.
Cal seguir el mateix mecanisme que amb les interrelacions ternàries amb connectivitat 1-M-N, 1-1-N i 1-1-1.
4. Recursives. Les interrelacions recursives traduïdes es comporten de la mateixa manera que la de la resta d’interrelacions:
- Les binàries amb connectivitat 1-1 i 1-N donen lloc a una clau forana.
- Les binàries amb connectivitat M-N i les n-àries originen una nova relació.
a. Binàries amb connectivitat 1-1 o 1-N. En aquestes situacions, cal afegir a la relació sorgida de l’entitat originària que es relaciona amb ella mateixa una clau forana que faci referència a la pròpia clau primària.
Evidentment, els atributs de la clau forana no poden tenir els mateixos noms que els de la clau primària als quals fan referència, ja que tots dos es troben en la mateixa relació, i això atemptaria contra els principis del model relacional.
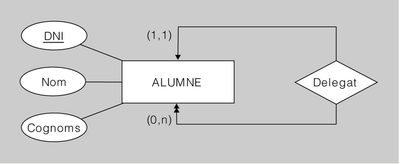
Exemple de transformació d'interrelació recursiva binària amb connectivitat 1-N
El diagrama ER de la figura.9 es tradueix al model relacional de la manera següent:
ALUMNE(DNI, Nom, Cognoms, DNIDelegat) ON {DNIDelegat} REFERENCIA ALUMNE
---
b. Binàries amb connectivitat M-N. Quan la interrelació recursiva binària té connectivitat M-N s’origina una nova relació, la qual té com a clau primària els atributs que formen la clau primària de l’entitat originària, però dos cops, ja que cal modelitzar el fet que l’única entitat que intervé en la conceptualització prevista s’interrelaciona amb ella mateixa (i no pas amb una altra de diferent).
Cal modificar convenientment els noms d’aquests atributs que són presents dos cops en la nova relació perquè no coincideixin, i respectar així les directrius del model relacional.
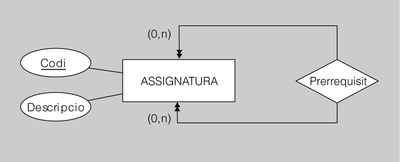
Exemple de transformació d'interrelació recursiva binària amb connectivitat M-N
El diagrama ER de la figura.10 es tradueix al model relacional de la manera següent:
ASSIGNATURA (Codi, Descripcio)
----
PRERREQUISIT(CodiAssignatura, CodiPrerrequisit) ON {CodiAssignatura} REFERENCIA ASSIGNATURA i
---------------------------------
{CodiPrerrequisit} REFERENCIA ASSIGNATURA
c. n-àries. S’origina una nova relació, la clau primària de la qual es construeix de manera diferent en funció de la connectivitat:
Quan la connexió de totes les entitats es produeix amb cardinalitat N, la clau primària de la nova relació es compon de tots els atributs que formen part de les claus primàries de totes les entitats interrelacionades (n).
Quan la connexió d’una o més de les entitats es produeix amb cardinalitat 1, la clau primària de la nova relació es compon de tots els atributs que formen les claus primàries de totes les entitats interrelacionades excepte una (n-1). L’entitat que no incorpora la seva clau primària a la de la nova relació ha d’estar forçosament connectada amb un 1.
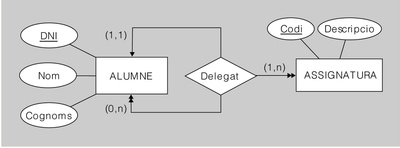
Exemple de transformació d'interrelació recursiva n-ària
El diagrama ER de la figura.11 es tradueix al model relacional de la manera següent:
ALUMNE(DNI, Nom, Cognoms)
---
ASSIGNATURA(Codi, Descripcio)
----
DELEGAT(DNIAlumne, CodiAssignatura, DNIDelegat) ON {DNIAlumne} REFERENCIA ALUMNE,
--------------------------
{CodiAssignatura} REFERENCIA ASSIGNATURA i {DNIDelegat} REFERENCIA ALUMNE
Fixem-nos que hem incorporat a la clau primària de la nova relació els atributs que
formen les claus primàries de les dues entitats connectades amb cardinalitat N, és a
dir, ASSIGNATURA i ALUMNE, però des de la posició dels alumnes que no són delegats.
D’aquesta manera, es modelitza el fet que cada alumne té un delegat per a cada assignatura,
i que el delegat de cada assignatura representa una pluralitat d’alumnes.
Entitats febles
Com que les entitats febles sempre estan situades en el costat N d’una interrelació 1-N que els serveix per completar la identificació inequívoca de les seves instàncies, la relació derivada de l’entitat feble ha d’incorporar a la seva clau primària els atributs que formen la clau primària de l’entitat de la qual són tributàries. Els atributs esmentats constitueixen, simultàniament, una clau forana que fa referència a l’entitat de la qual depenen.
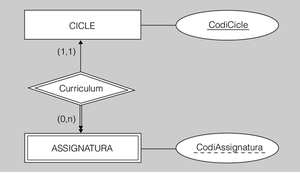
Exemple de transformació d'entitat feble
El diagrama ER de la figura.12 es tradueix al model relacional de la manera següent:
CICLE(CodiCicle)
---------
ASSIGNATURA(CodiCicle, CodiAssignatura) ON {CodiCicle} REFERENCIA CICLE
--------------------------
Generalització i especialització
En aquests casos, tant l’entitat superclasse com les entitats de tipus subclasse es transformen en noves relacions.
La relació derivada de la superclasse hereta d’aquesta la clau primària. A més, s’encarrega d’emmagatzemar els atributs comuns a tota l’especialització o generalització.
Les relacions derivades de les entitats de tipus subclasse també tenen, com a clau primària, la clau de l’entitat superclasse, que al mateix temps actua com a clau forana, en referenciar l’entitat derivada de la superclasse.
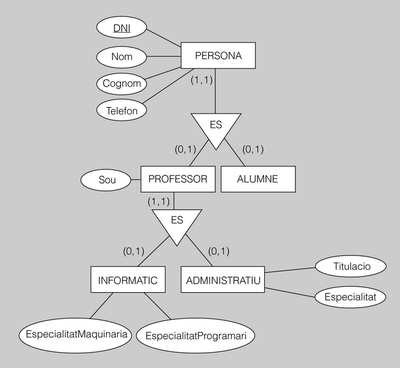
Exemple de transformació de generalització o especialització
La figura.13 mostra un encadenament de generalitzacions o especialitzacions. Si el
traduïm a un model relacional obtenim el resultat següent:
PERSONA(DNI, Nom, Cognoms, Telefon)
---
PROFESSOR(DNI, Sou) ON {DNI} REFERENCIA PERSONA
---
ALUMNE(DNI) ON {DNI} REFERENCIA PERSONA
---
INFORMATIC(DNI, EspecialitatMaquinari, EspecialitatProgramari) ON {DNI} REFERENCIA PROFESSOR
---
ADMINISTRATIU(DNI, Titulacio, Especialitat) ON {DNI} REFERENCIA PROFESSOR
---
Entitats associatives
Les entitats associatives es basen en una interrelació entre entitats. La traducció d’aquesta interrelació a un model relacional equival a la traducció de l’entitat associativa.
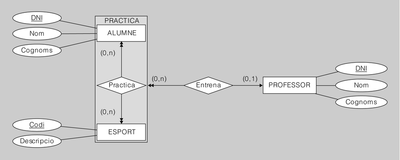
Exemple de transformació d'entitat associativa
El diagrama ER de la figura.14 es tradueix al model relacional de la manera següent:
ALUMNE(DNI, Nom, Cognoms)
---
ESPORT(Codi, Descripcio)
----
PROFESSOR(DNI, Nom, Cognoms)
---
PRACTICA(DNIAlumne, CodiEsport, DNIProfessor) ON {DNIAlumne} REFERENCIA ALUMNE, {CodiEsport}
---------------------
REFERENCIA ESPORT i {DNIProfessor} REFERENCIA PROFESSOR
Fixem-nos com la relació PRACTICA, derivada de l’entitat associativa, incorpora una clau forana
que fa referència a la relació PROFESSOR, ja que l’entitat associativa originària és al costat
N d’una interrelació binària amb l’entitat PROFESSOR.