ASIX-M3-UF2-A1.1-Exercicis disseny descendent

1. Regne de Dracs

En aquest joc, el jugador es troba en una terra de dracs. Els dracs viuen en coves i hi ha de dos tipus: els bons que volen compartir els seus tesors amb tu i els dolents molt cobdiciosos i afamats que no dubtaran a menjar-se tot aquell que provi d'accedir a la seva cova. El jugador es troba davant de dues coves, en una el drac amigable i en l'altre el drac dolent. El jugador a d'escollir...

• Mòduls a emprar:

from random import randint  # per distribuir els dracs en les coves aleatoriament
from time import sleep      # per fer més "emocionant" el final del joc

• El programa principal podria ser semblant a:

# Programa principal 
fiJoc = False
while not fiJoc:
    mostrarIntroduccio()
    numeroDeCova = escollirCova()
    explorarCova(numeroDeCova)    # sleep(2)   # randint(1, 2)
    jugarDeNuevo = jugar()

2. Construir un Quadrat màgic. Un quadrat màgic és una matriu quadrada (mateix nombre de files que de columnes), amb un nombre senar de files i columnes on la suma dels elements de totes les seves files i les seves columnes i les dues diagonals val igual. En aquest quadrat no hi ha cap número repetit, i els números que hi ha d'haver han d'anar des de 1 fins a n² on n és el numero de files i columnes.

Com construir-lo?

• El numero 1 el situarem en el quadrat superior al central (per exemple, per n=5, el quadrat central és (2,2) i el que està per sobre seu el (1,2).

• El següent número el situarem un quadrat a la dreta i un per sobre. Si un numero està a la posició (i,j), el següent el situarem en (i-1,j+1).

• Si resulta que al fer el moviment sortim per la dreta, entendrem que automàticament entrarem per l'esquerra, és a dir, és com si la matriu estigués enganxada la part esquerra amb la part dreta. El mateix passa amb dalt i baix. Si sortim per dalt, entrem per baix.

• A més ens podem trobar que la posició on toca anar un número ja es troba ocupada. Llavors el que farem és tornar a la posició on estàvem i fer el moviment que puja dos posicions (i-2, j ).

• Un exemple de quadrat màgic per a N=5 seria:

      23  6 19  2 15
      10 18  1 14 22
      17  5 13 21  9
       4 12 25  8 16
      11 24  7 20  3

• El programa tindrà les següents funcions:

llegirDimensio: Li demanem a l’usuari que ens indiqui la mida N de la matriu. Si el valor és correcte, la funció el retorna.

inicialitzarQuadrat: Simplement posem tots els valors a 0

calculaPosicioInicial: Segons la dimensió, calculem la primera posició

assignaValor: Posa un valor en una posició

calcularNovaPosicio: Retorna els valors de fila i columna vàlids per a col·locar el proper valor.

imprimirQuadrat: Treu per pantalla el quadrat màgic,

• El programa serà semblant a aquest :

dim = llegirDimensio()
qm = inicialitzarQuadrat(dim)
pos = calculaPosicioInicial(dim)
limit = dim*dim;
for valor in range(1,limit+1):
   assignaValor(qm,pos,valor)
   pos = calcularNovaPosicio(qm, dim, pos) 
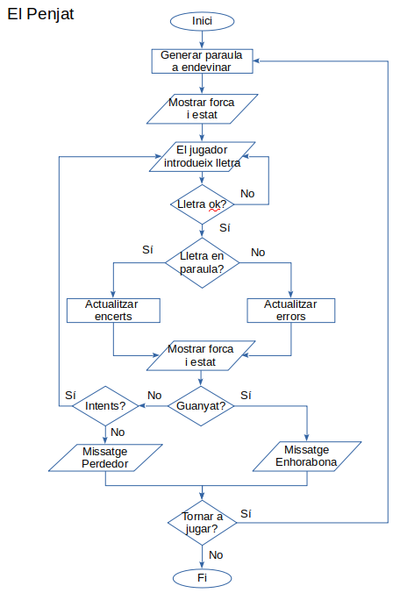
imprimirQuadrat(qm)

3. El Penjat

El penjat consisteix en endevinar una paraula generada aleatòriament per l'ordinador. Dinàmica del joc:

• Es presenta una forca i un guio per a cada lletra de la paraula.
• El jugador proposa lletres (d'una en una) i:

• si la lletra es troba a la paraula es substitueixen els guions respectius per la lletra.
• sinó s'actualitza la forca en una part del cos (cap, tronc, braç esquerra, braç dret, cama esquerra i cama dreta).

• El joc finalitza quan es troben totes les lletres o quan ja no queden parts del cos.
• El programa permetre tornar a jugar si així o vol el jugador.
• Diagrama de flux