Diferència entre revisions de la pàgina «ASIX-M3-UF2-A1.2-Pràctiques disseny descendent»
(→Atributs dels lluitadors) |
(→El paquet "joc.arena.regles") |
||
| Línia 222: | Línia 222: | ||
Un cop es disposa d’aquesta divisió, cada cop que calgui implementar un subproblema en forma de mètode, caldrà fer-ho a la classe que correspongui d’acord a aquesta distribució de tasques. | Un cop es disposa d’aquesta divisió, cada cop que calgui implementar un subproblema en forma de mètode, caldrà fer-ho a la classe que correspongui d’acord a aquesta distribució de tasques. | ||
| − | ==El paquet "joc.arena.regles"== | + | ===El paquet "joc.arena.regles"=== |
| − | ===La classe Monedes=== | + | ====La classe Monedes==== |
| − | ===La classe Lluitador=== | + | ====La classe Lluitador==== |
| − | ====Mètodes vinculats a l'estat del lluitador==== | + | =====Mètodes vinculats a l'estat del lluitador===== |
===La classe Bestiari=== | ===La classe Bestiari=== | ||
Revisió del 19:53, 27 feb 2021
Contingut
Pràctica 1: Els bacteris
Un laboratori d’investigació cultiva una colònia de bacteris dins d’una àrea que es pot considerar com una superfície quadriculada de dimensió 30 x 30. Cada casella pot ser buida o contenir un bacteri. A partir de la seva configuració inicial, la colònia evoluciona generació rere generació segons unes lleis genètiques que tot seguit es descriuen i que depenen del nombre de veïns que té cada casella:
- Naixement: tota casella buida amb exactament tres veïns tindrà un naixement la propera generació.
- Mort per solitud: tot bacteri que ocupa una casella amb 0 o 1 veïns morirà per solitud la propera generació.
- Supervivència: tot bacteri que ocupa una casella amb 2 o 3 veïns sobreviurà la propera generació.
- Mort per asfixia: tot bacteri que ocupa una casella amb més de 3 veïns morirà per asfixia la següent generació.
Noteu que cada bacteri té com a molt 8 veïns i que en el cas dels bacteris residents a les vores de la quadrícula el nombre de veïns és menor. Es considera que la transició entre generacions és simultània en totes les caselles de la colònia. Es demana dissenyar un programa que simuli l’evolució de la colònia de bacteris i determini, a partir d’una situació inicial aleatòria, quantes iteracions es necessiten per tal que la colònia arribi a una situació estable.
El programa serà semblant al següent:
Programa bacteris
Inicialitzar variables
Generar generació inicial
Mostrar generació inicial
Mentre no situació estable fer
Generar següent generació
situació estable =(generació actual = =següent generació)
generació actual = següent generació
fMentre
Mostrar generació final
Mostrar nombre d’iteracions realitzades
fPrograma
Aclariments sobre algunes funcions
- El procediment Generar generació inicial ha de crear una colònia de forma aleatòria. La forma més senzilla en és omplir la matriu amb valors aleatoris. Random r =new Random(); r.nextInt(2) i us retornarà valors que seran o bé 0 o bé 1 (podeu considerar per exemple que 1 representa que hi ha un bacteri i 0 que no).
- El procediment Mostrar generació inicial simplement traurà per pantalla l’estat actual. No cal fer virgueries en la presentació, simplement que s’entengui el que hi ha. El procediment Mostrar generació final és exactament el mateix, simplement canviarà el paràmetre que li passem.
- El procediment Generar següent generació ens crea la nova generació seguint les regles explicades abans. Òbviament per poder-ho fer haurà de cridar a una funció veïns que ens indiqui per a cada posició de la matriu, quants veïns n’hi ha.
Considerem que la situació és estable quan després de crear una nova generació ja no hi ha canvis a la colònia.
Aquest sistema genètic funciona, però per possibles errors de programació podria ser que entrés en un bucle infinit, per això fins que no esteu segurs que el programa funciona i acaba bé podeu posar també com a condició del bucle que no doni més de 500 voltes. També és cert que en algun cas pot entrar en un cicle de dues voltes i per tant serà millor que poseu sempre aquesta condició.
Si no teniu clar on falla el programa, es pot dintre del bucle visualitzar cada vegada el tauler, però això ralentitzarà molt l’execució. Si ho voleu provar d’aquesta manera, feu-lo amb matrius petites ( 6 x 6 o així). Quant tingueu clar que funciona, torneu a donar la mida inicial.
NOTES: El programa ha d’estar perfectament estructurat i la filosofia és l’explicada abans. No cal que sigui exactament així però penso que no pot canviar molt l’estructura. Tot ha de fer-se mitjançant funcions (potser Inicialitzar variables no cal) i heu de pensar que el programa principal no quedarà gaire més llarg que el programa de la pàgina anterior. Cal comentar el codi.
Pràctica 2: Combat a l'arena
El joc de combats a l'arena
El programa que serveix com a fil argumental d’aquest apartat és un joc, en el qual el jugador es va enfrontant amb diversos adversaris en una arena. Cada combat es divideix en rondes, a l’inici de les quals el jugador i el seu adversari trien secretament una estratègia a seguir. Cada ronda pot seguir una estratègia diferent. Segons les estratègies triades per cadascú, el combat s’anirà resolent més favorablement cap a un o cap a l’altre, fins que finalment es consideri que un dels dos ha estat derrotat. Si es derrota l’adversari, s’atorga una puntuació al jugador. Si el jugador és derrotat, acaba la partida.
L’objectiu final del jugador és sobreviure deu combats, assolint la màxima puntuació possible en el procés.
Tant per mostrar dades a l’usuari com per introduir les ordres del jugador, s’usa només text.
Funcionament del joc de combats a l'arena
- Descarregue-vos del Moodle el fitxer JocDeCombat.jar.
- Accediu per terminal a la carpeta on es troba el fitxer.
- Executeu-lo: java -jar JocDeCombat
Atributs dels lluitadors
Per descriure tots els lluitadors, tant el jugador com els seus adversaris, aquests disposen d’un seguit d’atributs que indiquen el seu estat en tot moment. Alguns d’aquests atributs serveixen per establir com progressa el combat i poden veure modificats els seus valors.
Tot seguit s’enumeren:
- Nom: el nom del lluitador. Per al jugador és “Aventurer”, mentre que per als adversaris es referirà a criatures fantàstiques (“Nan”, “Ogre”, “Hidra”, etc.)
- Nivell: indicador general de la capacitat de combat del lluitador.
- Punts: els punts que ha acumulat el lluitador fins al moment.
- Punts de Vida (PV): l’energia del lluitador actual, que pot variar al llarg del combat. Quan arriba a 0 o menys, es considera derrotat.
- Punts de Vida Màxims: valor màxim que poden tenir els punts de vida en qualsevol moment.
- Atac: la seva capacitat de dur a terme amb èxit estratègies ofensives. S’usa per resoldre el resultat d’una ronda de combat.
- Defensa: igual que l’anterior, però per a estratègies defensives.
El programa es basa en què el jugador va realitzant un combat rere l’altre contra diferents adversaris. Per guanyar, ha de sobreviure a deu combats. Fins que no acaba un combat, i s’ha decidit si el jugador l’ha guanyat o l’ha perdut, no es comença un de nou.
A l’inici de cada combat, es mostra l’estat actual del jugador, el valor actual de tots els seus atributs, i se li pregunta contra quin adversari vol lluitar. El jugador ha d’escriure el nom d’un adversari. Si aquest nom no es troba entre el dels adversaris disponibles en el joc, iniciarà un combat contra un triat a l’atzar entre tots els adversaris disponibles del seu mateix nivell o un de diferència. Això evita que, per sorpresa, es trobi que ha de lluitar contra un adversari massa poderós per a ell, impossible de guanyar.
Si el nom pertany a algun adversari disponible, llavors s’enfronta contra ell. En aquest cas, no hi ha cap restricció de nivell. El jugador pot triar lluitar contra adversaris molt més o menys poderosos que ell.
Aquest plantejament està disposat de manera que, d’entrada, un nou jugador no sap el nom de cap adversari, ja que no es proporciona cap llista (a menys que hagi fet el programa o vist el codi font, és clar). La intenció és que vagi descobrint nous noms d’adversaris a mesura que va jugant partides, o parlant amb amics que també juguin al joc.
Resolució d'una ronda de combat
Cada combat es divideix en un seguit de rondes, en cadascuna de les quals el jugador ha de triar quina estratègia vol usar. Al principi de cada ronda es mostra l’estat actual tant del jugador com del seu adversari, de manera que sigui possible avaluar quina via d’acció li pot convenir més dur a terme. Llavors, el jugador tria l’estratègia entre quatre possibles: Atacar, Defensar, Engany i Maniobra. Un cop triada, l’adversari en triarà la seva i es decidirà el resultat de la ronda.
Primer de tot, cal veure per a cada lluitador el grau d’èxit de la seva estratègia. Si ha triat Atacar o Engany, representa que llença tantes monedes com el seu valor d’Atac. Si ha triat Defensar o Maniobra, fa el mateix usant el seu valor de Defensa. El grau d’èxit serà el nombre de cares obtingudes.
En resoldre la ronda, cada lluitador pot rebre un dels efectes següents. La gravetat de cadascun d’ells depèn del grau d’èxit del lluitador mateix o del seu con trincant.
En resoldre la ronda, cada lluitador pot rebre un dels efectes següents. La gravetat de cadascun d’ells depèn del grau d’èxit del lluitador mateix o del seu con trincant.
- Res: no passa res.
- Danyat: el lluitador perd una quantitat de punts de vida igual al grau d’èxit del contrincant.
- Guarit: el lluitador recupera tants punts de vida, sense superar mai el valor màxim, com el seu propi grau d’èxit.
- Penalitzat: el lluitador veu penalitzat el seu valor d’atac o de defensa (es tria a l’atzar) en tants punts com el grau d’èxit del contrincant. La penalització mai pot fer baixar el valor per sota d’1. Aquest efecte dura fins a la propera ronda múltiple de cinc (5, 10, 15, etc.). Llavors, retorna al seu valor original.
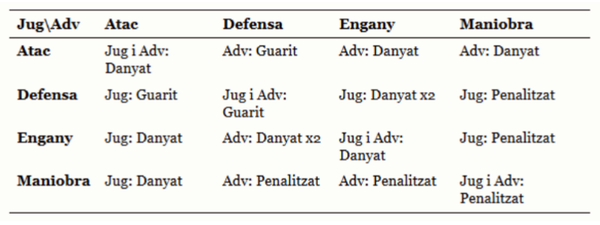
L’efecte que rep cada lluitador depèn de les interaccions entre les estratègies, de manera semblant al joc de pedra, paper, tisores. Depenent de l’estratègia triada i la de l’adversari, el resultat serà diferent. La taula següent mostra el resultat de les interaccions entre estratègies. Per abreujar, “Jug” es refereix al jugador i “Adv” a l’adversari. Un indicador de “x2” vol dir que a l’hora de resoldre aquest efecte, es doblen els èxits assolits pel contrincant.
Exemple de ronda de combat
Per exemple, suposeu que el jugador té ara mateix 10 punts de vida i els seus valors d’atac i defensa són 4 i 3, respectivament. L’adversari té 6 punts de vida i els seus valors d’atac i defensa són 3 i 5 respectivament. Primer de tot, cadascú tria la seva estratègia. El jugador tria Atac mentre que l’adversari tria Maniobra. Això vol dir que, per veure el grau d’èxit, el jugador llençarà tantes monedes com el seu Atac i l’adversari, en haver triat Maniobra, tantes com la seva defensa. El jugador llença 4 monedes i suposeu que treu dues cares. L’adversari en llença 5 i suposeu que n’obté quatre.
Ara cal veure l’efecte de les estratègies. D’acord a la taula, si el jugador tria Atac i l’adversari tria Maniobra, el resultat és que l’adversari rep l’efecte de “Danyat” (Adv: Danyat). Se li descompten tants punts de vida com el grau d’èxit del jugador (2). Per tant, ara li queden 6 - 2 = 4 punts de vida i acaba aquesta ronda.
S’inicia una nova ronda on es mostra l’estat dels dos lluitadors i es tria una nova estratègia...
Evidentment, a l’hora de triar l’estratègia, l’ordinador no hauria de fer trampes (ja que coneixerà la del jugador abans de triar-ne la seva). Es pot triar a l’atzar, o seguint alguna tàctica segons el seu estat (defensar més sovint si li queden pocs punts de vida, enganyar si el jugador defensa molt sovint, etc.). Això depèn del grau d’intel·ligència que es vol que tingui l’ordinador.
Resolució de la finalització del combat
El combat finalitza quan, en acabar una ronda, un del lluitadors té 0 o menys punts de vida. Si es tracta del jugador, es considera derrotat. La partida acaba i es mostra la seva puntuació final. Aquesta circumstància inclou també el cas d’empat (ambdós lluitadors han arribat a 0 punts de vida). Si, en cas contrari, és l’adversari el derrotat, al personatge se li atorga certa quantitat de punts, que se sumen als que ja disposa. Els punts atorgats dependran dels punts de l’adversari i, normalment, adversaris més difícils tindran sempre punts.
En atorgar punts al jugador, si aquest arriba o supera un valor associat a una centena (100, 200, 300, etc.), es considera que “puja de nivell” i es fa més poderós. Quan això succeeix, el jugador veu incrementat en un punt el seu nivell, el seu màxim de punts de vida s’incrementa en dos, i el seu atac o defensa, un dels dos triat a l’atzar, s’incrementa en un punt. El jugador també és immediatament guarit, recuperant tots els punts de vida actuals fins a aquest nou màxim.
Un cop atorgats els punts i un possible increment del seu nivell, totes les penalitzacions actuals sobre el jugador desapareixen. Ara bé, a menys que hagi pujat de nivell, aquest no recupera cap punt de vida. Començarà el combat següent amb exactament els mateixos punts amb els quals ha finalitzat aquest.
Si aquest era el desè combat, la partida acaba amb un missatge de felicitació i es mostra la puntuació final. En cas contrari, es torna a iniciar un nou combat.
Identificació de les dades a tractar
De la descripció del problema, les dades principals que cal tractar són les dels dos lluitadors, el jugador i els seus adversaris, que seran les mateixes. Afortunadament, la descripció del problema ofereix una visió clara de quina mena de valors cal manipular (Nom, Nivell, Vida, etc.). En aquest cas, atès que són força valors, tots vinculats entre ells, el més fàcil és fer servir una taula, de manera que es gestioni una per al jugador i una per a l’adversari. D’aquesta manera, amb un parell de variables és senzill disposar de totes les dades vinculades a tots dos. Cada posició de la taula pot representar cadascun dels atributs.
Per exemple:
public final static int IDENTIFICADOR = 0;
public final static int NIVELL = 1;
public final static int PUNTS = 2;
public final static int VIDA = 3;
public final static int VIDA_MAX = 4;
public final static int ATAC = 5;
public final static int ATAC_MAX = 6;
public final static int DEFENSA = 7;
public final static int DEFENSA_MAX = 8;Disseny descendent
En aquest cas, l’objectiu principal del problema plantejat és veure com crear aplicacions complexes de manera modular. Per tant, no es durà a terme un disseny descendent complet fins al darrer detall, sinó que aquest servirà per fer un esquema clar de quines són les accions que ha de dur a terme el programa i, en alguns casos, en quin ordre. Per tant, aquest apartat també té un paper de suport a l’hora de presentar-vos el problema perquè l’entengueu.
De la descripció del problema general, se’n podrien extreure els subproblemes enumerats tot seguit. Recordeu, però, que potser aquesta no és l’única solució vàlida, és una proposta d’interpretació possible de l’enunciat. Hi poden haver altres descomposicions vàlides.
1. Generar els atributs del nou jugador.
2. Anunciar inici del combat.
(a) Mostrar estat del jugador.
3. Triar l’adversari.
4. Combatre.
(a) Mostrar estat dels lluitadors.
i. Mostrar estat del jugador.
ii. Mostrar estat de l’adversari.
(b) Triar estratègia del jugador.
(c) Triar estratègia de l’adversari.
(d) Resoldre resultats d’estratègies.
i. Llençar monedes.
ii. Penalitzar lluitador.
iii. Danyar lluitador.
iv. Guarir lluitador.
(e) Restaurar lluitador.
5. Resoldre resultat del combat.
(a) Atorgar puntuació.
(b) Pujar de nivell.
(c) Finalització del joc.Aquesta llista ja dóna una bona idea del conjunt de tasques que cal fer. En aquest cas, a mesura que es vagi resolent cada subproblema, si es considera que encara és massa complex o resulta que és un mètode massa llarg, ja es faran noves descomposicions en el mateix moment. Aquesta és una estratègia acceptable per a programes complexos, ja que la descomposició es pot fer molt complicada, en ser difícil veure realment tots els detalls i tenir una idea clara de la mida o complexitat dels mètodes resultants. Però al menys, sempre heu de tenir la disciplina de fer una primera aproximació, per generar el codi font amb una idea clara de per on començar.
Abans de seguir, val la pena fer alguns comentaris. Els subproblemes 4.b i 4.c s’han considerat diferents ja que, si us hi fixeu, hauran de dur a terme tasques força diferents.
En el cas del jugador, es pregunta directament a l’usuari, mentre que en el cas de l’adversari l’ordinador és qui l’ha de generar d’alguna manera (per exemple, simplement a l’atzar). En canvi, per al cas dels subproblemes 4.a.i i 4.a.ii, de ben segur que faran el mateix. Només canviaran les dades a tractar. Per tant és un cas clar de parametrització d’un mètode. Per acabar, aquest plantejament també reaprofita subproblemes, ja que el 4.a.i i el 2.a són exactament el mateix.
Mòduls
Si es vol considerar una aproximació modular, un cop es coneixen les tasques que ha de dur a terme el programa en forma de subproblemes, el pas següent seria agrupar-les d’acord al tipus d’accions que porten a terme. Cada conjunt serà un mòdul diferent. En aquest cas, atès que el programa es fa en Java, ja s’usarà directament una organització en classes i paquets.
Com a punt de partida, caldria escollir un nom de paquet general per a tot el programa. Aquest serà joc.arena. La classe principal anirà aquí.
A continuació, cal escollir si es vol usar una jerarquia de paquets que parteixi de la base per ordenar totes les classes o no. Per a aquest cas, sol ser una bona política dividir les parts vinculades amb la interfície d’usuari de les que estan lligades a la manipulació de les dades del programa. En separar els aspectes relacionats amb la presentació de les dades del seu tractament, els canvis en els mòduls d’un programa (per exemple, passar d’una interfície textual a una gràfica) no afecten el codi dels mòduls de l’altre. Aquesta divisió es pot fer usant dos paquets: joc.arena.regles i joc.arena.interficie.
Ara és el moment de dividir les tasques que ha de fer el programa en classes i triar a quin paquet anirà cadascuna.
Per a aquest problema es proposa la divisió següent en mòduls. Al paquet joc.arena.regles hi haurà les classes:
- Monedes: per a les tasques vinculades al llançament de monedes per resoldre una ronda.
- Lluitador: per a les tasques vinculades a la manipulació de les dades d’un lluitador (danyar, guarir, etc.).
- Bestiari: per a les tasques vinculades a la generació d’adversaris i el jugador.
- Combat: per a les tasques vinculades a la resolució d’estratègies enfrontades.
Al paquet joc.arena.interficie es decideix dividir les classes que tracten la pantalla i el teclat, de manera que hi haurà:
- EntradaTeclat: s’encarrega de les tasques importants que són donades pel que escriu l’usuari usant el teclat.
- SortidaPantalla: com l’anterior, però per mostrar informació a pantalla.
La classe principal, JocArena és al paquet que engloba els anteriors, joc.arena, donada la jerarquia de noms.
Un cop es disposa d’aquesta divisió, cada cop que calgui implementar un subproblema en forma de mètode, caldrà fer-ho a la classe que correspongui d’acord a aquesta distribució de tasques.