Diferència entre revisions de la pàgina «ASIX-M3-UF2-Banc de Solucions»

De wikiserver
Dreceres ràpides: navegació, cerca
(→‎3 en ratlla)
 
(Hi ha 11 revisions intermèdies del mateix usuari que no es mostren)
Línia 696: Línia 696:
 
     jugar = jugarDeNou()
 
     jugar = jugarDeNou()
 
</source>
 
</source>
 +
-->
 +
 +
==Recursivitat==
 +
<!--
 +
0. Fes un meńu per escollir l'exercici a executar: el menú es trobarà en un fitxer diferent dels exercicis i aquests s'ubicaran en el mateix mòdul.
 +
 +
<source lang="python">
 +
from recursivitat import * #Importem totes les funcions explícites del mòdul recursivitat
 +
 +
def menu(*args):
 +
    opcions = []
 +
    print("")
 +
    for opcio in args:
 +
        print(opcio)
 +
        opcions.append(opcio[:1])
 +
    print("")
 +
    op = input("Escull opció: ")
 +
    while op not in opcions:
 +
        op = input("Escull opció: ")
 +
    return op
 +
 +
opc = menu("1. Sumatori", "2. Potència", "3. Suma Digital", "4. MCD", "5. Suma Harmònica", "6. Existeix Dígit")
 +
if opc=="1":
 +
  digits = int(input("Introdueix el número de enters a sumar: "))
 +
  print("Resultat suma dels %d primers números naturals: " %digits, sumatori(digits))
 +
elif opc=="2":
 +
  num = int(input("Introdueix un número: "))
 +
  pot = int(input("Introdueix la potència: "))
 +
  print("Resultat de %d elevat a %d: " %(num, pot), potencia(num, pot))
 +
if opc=="3":
 +
  num = int(input("Introdueix un número per sumar els seus dígits: "))
 +
  print("Resultat suma dels dels dígits del número %d: " %num, sumaDigital(num))
 +
if opc=="4":
 +
  num1 = int(input("Introdueix un número: "))
 +
  num2 = int(input("Introdueix un segon número: "))
 +
  print("MCD dels números %d i %d és: " %(num1, num2), mcd(num1,num2))
 +
if opc=="5":
 +
  num = int(input("Introdueix un número per fer la seva suma harmònica: "))
 +
  print("Resultat de la suma harmònica del número %d: " %num, sumaHarmonica(num))
 +
if opc=="6":
 +
  num = int(input("Introdueix un número: "))
 +
  digit = int(input("Introdueix un dígit: "))
 +
  print("Existeix el dígit %d en el número %d: " %(digit, num), existeixDigit(num,digit))
 +
</source>
 +
 +
1. Escriure una funció recursiva que donat un número N (N ≥ 0) passat com a paràmetre calculi la suma de tots els números enters fins a N inclòs.
 +
<source lang="python">
 +
def sumatori(n):
 +
    suma = 0;
 +
    if n > 0:
 +
      suma = n + sumatori(n - 1)
 +
    return suma
 +
</source>
 +
 +
2. Escriure una funció recursiva que calculi el resultat de X elevat a N amb N >0, sabent que X0 = 1.
 +
<source lang="python">
 +
def potencia(num, pot):
 +
    res = 1;
 +
    if pot > 0:
 +
      res = potencia(num, pot - 1) * num
 +
    return res
 +
</source>
 +
 +
3. Escriu una funció recursiva per calcular la suma digital d’un número natural. Per exemple, la suma digital de 18624 és: 4 + 2 + 6 + 8 + 1 = 21
 +
<source lang="python">
 +
def sumaDigital(n):
 +
    if n < 10:
 +
      suma = n
 +
    else:
 +
      suma = sumaDigital(n // 10)
 +
      suma = suma + n % 10
 +
    return suma
 +
</source>
 +
 +
4. Dissenyeu un algoritme recursiu que calculi el màxim comú divisor de dos enters positius, sabent que :
 +
<pre>
 +
    MCD( X, Y) = MCD (X-Y, Y) SI X > Y
 +
    MCD (X, Y-X) SI Y > X
 +
    X SI X = Y
 +
</pre>
 +
<source lang="python">
 +
def mcd(x, y):
 +
    if x==y:
 +
      return x
 +
    elif x > y:
 +
      return mcd(x - y, y)
 +
    else:
 +
      return mcd(x, y - x);   
 +
</source>
 +
   
 +
5. Fes la funció recursiva SumaHarmonica (n) que retorna la suma:
 +
<pre>
 +
    1 + 1/2 +1/3 + ... + 1/n
 +
</pre>
 +
<source lang="python">
 +
def sumaHarmonica(n):
 +
    suma=0.0
 +
    if n>0:
 +
      suma=sumaHarmonica(n-1)+1.0/n
 +
    return suma
 +
</source> 
 +
 
 +
6. Fes una funció recursiva booleana que donats un número i un dígit retorni si aquest dígit pertany al número. Per exemple:
 +
<pre>
 +
  existeix(1234,3) → true
 +
  existeix(1234,7) → false
 +
</pre>
 +
<source lang="python">
 +
def existeixDigit(numero, dig):
 +
    exist=False;
 +
    if numero > 0:
 +
      exist=(numero % 10 == dig) or existeixDigit(numero // 10, dig)
 +
    return exist;
 +
</source> 
 +
 +
7. Fes una funció que calculi el producte segons el mètode rus que diu que:
 +
<pre>
 +
    x*y = ((2*x) *(y/2)) SI y es parell
 +
    x*y =((2*x) *(y/2))+ x SI y és senar.
 +
 +
    Quan y val 1, el resultat és x.
 +
</pre>
 +
    public int producteRus(int x, int y) {
 +
        if (y == 1) {
 +
            return x;
 +
        } else if (y % 2 == 0) {
 +
            return producteRus(2 * x, y / 2);
 +
        } else {
 +
            return producteRus(2 * x, y / 2) + x;
 +
        }
 +
    }
 +
 +
 +
}
 +
8. Torres de Hanoi (amb N introduïda per l’usuari com a paràmetre). S’ha d’anar visualitzant la solució per pantalla.
 +
 +
9. Fes una funció recursiva que ompli un tauler n-goro. Un tauler n-goro és una matriu de n files i n+1 columnes que s'omple consecutivament en diagonal i quan ens sortim per una banda entrem per l'altra. L'últim element que s'omple serà l'extrem inferior dret.
 +
<pre>
 +
    Per exemple amb n=3
 +
 +
      1 10 7 4
 +
      5 2 11 8
 +
      9 6 3 12
 +
 +
    Amb n = 4
 +
 +
      1 17 13 9 5
 +
      6 2 18 14 10
 +
      11 7 3 19 15
 +
      16 12 8 4 20
 +
</pre>
 +
<!--
 +
Soluciones
 +
 +
https://foro.elhacker.net/ejercicios/ejercicios_recursivos_en_java_y_sus_soluciones-t231013.0.html
 
-->
 
-->

Revisió de 19:17, 23 març 2021

Regne de Dracs

En aquest joc, el jugador es troba en una terra de dracs. Els dracs viuen en coves i hi ha de dos tipus: els bons que volen compartir els seus tesors amb tu i els dolents molt cobdiciosos i afamats que no dubtaran a menjar-se tot aquell que provi d'accedir a la seva cova. El jugador es troba davant de dues coves, en una el drac amigable i en l'altre el drac dolent. El jugador a d'escollir...

  • Mòduls a emprar:
from random import randint  # per distribuir els dracs en les coves aleatoriament
from time import sleep      # per fer més "emocionant" el final del joc

Quadrat màgic

Construir un Quadrat màgic. Un quadrat màgic és una matriu quadrada (mateix nombre de files que de columnes), amb un nombre senar de files i columnes on la suma dels elements de totes les seves files i les seves columnes i les dues diagonals val igual. En aquest quadrat no hi ha cap número repetit, i els números que hi ha d'haver han d'anar des de 1 fins a n2 on n és el numero de files i columnes.

Com construir-lo?

  • El numero 1 el situarem en el quadrat superior al central (per exemple, per n=5, el quadrat central és (2,2) i el que està per sobre seu el (1,2).
  • El següent número el situarem un quadrat a la dreta i un per sobre. Si un numero està a la posició (i,j), el següent el situarem en (i-1,j+1).
  • Si resulta que al fer el moviment sortim per la dreta, entendrem que automàticament entrarem per l'esquerra, és a dir, és com si la matriu estigués enganxada la part esquerra amb la part dreta. El mateix passa amb dalt i baix. Si sortim per dalt, entrem per baix.
  • A més ens podem trobar que la posició on toca anar un número ja es troba ocupada. Llavors el que farem és tornar a la posició on estàvem i fer el moviment que puja dos posicions (i-2, j ).
  • Un exemple de quadrat màgic per a N=5 seria:
      23  6 19  2 15
      10 18  1 14 22
      17  5 13 21  9
       4 12 25  8 16
      11 24  7 20  3
  • El programa tindrà les següents funcions:
llegirDimensio: Li demanem a l’usuari que ens indiqui la mida N de la matriu. Si el valor és correcte, la funció el retorna.
inicialitzarQuadrat: Simplement posem tots els valors a 0
calculaPosicioInicial: Segons la dimensió, calculem la primera posició
assignaValor: Posa un valor en una posició
calcularNovaPosicio: Retorna els valors de fila i columna vàlids per a col·locar el proper valor.
imprimirQuadrat: Treu per pantalla el quadrat màgic,
  • El programa serà semblant a aquest :
dim = llegirDimensio()
qm = inicialitzarQuadrat(dim)
pos = calculaPosicioInicial(dim)
limit = dim*dim;
for valor in range(1,limit+1):
   qm = assignaValor(qm,pos,valor)
   pos = calcularNovaPosicio(qm, dim, pos) 
imprimirQuadrat(qm)

Mastermind

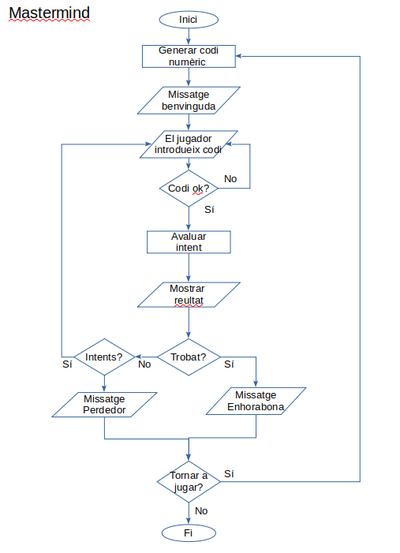
El Mastermind és un joc que consisteix en, mitjançant pistes, deduir un codi numèric de n xifres ocult (en el nostre cas de quatre xifres i generat aleatòriament). Dinàmica del joc:

  • El programa generà aleatòriament un codi numèric de quatre xifres (codi a endevinar).
  • El jugador anirà proposant codis (intents) per tal de trobar el codi a endevinar.
  • L'objectiu es trobar el codi en el menor número d'intents. Es pot limitar el número d'intents (per ex. a 7).
  • Desprès de cada intent el programa donarà pistes que ajudin a deduir el codi:
  • Encerts: quants números s'han encertat i es troben en la posició correcta .
  • Coincidències: quants números s'han encertat però no es troben en la posició correcta.
  • Exemple:
  • codi: 7539
  • proposta: 2590
  • pistes: 1 encert i 1 coincidència.
  • El joc finalitzarà quan s'hagi trobat el codi numèric o s'hagin exhaurit els intents.
  • El programa permetrà tornar a jugar si així o vol el jugador.
  • Diagrama de flux
Diagrama flux "Mastermind"


El Penjat

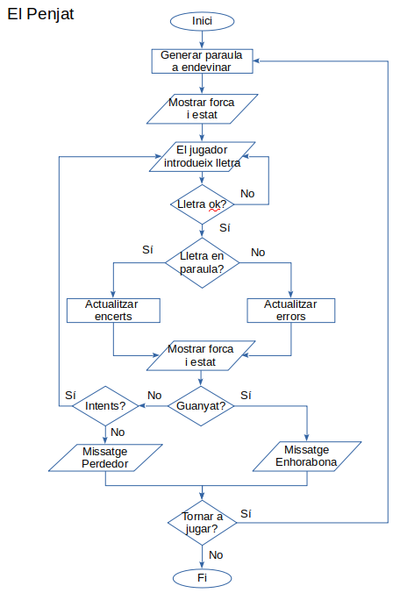
El penjat consisteix en endevinar una paraula generada aleatòriament per l'ordinador. Dinàmica del joc:

  • Es presenta una forca i un guio per a cada lletra de la paraula.
  • El jugador proposa lletres (d'una en una) i:
  • si la lletra es troba a la paraula es substitueixen els guions respectius per la lletra.
  • sinó s'actualitza la forca en una part del cos (cap, tronc, braç esquerra, braç dret, cama esquerra i cama dreta).
  • El joc finalitza quan es troben totes les lletres o quan ja no queden parts del cos.
  • El programa permetrà tornar a jugar si així o vol el jugador.
  • Diagrama de flux
Diagrama flux "El Penjat"

3 en ratlla

El joc consisteix en posar 3 fitxes en línia en un tauler de 9 caselles abans que ho faci l'ordinador.

  • El jugador i l'ordinador alternen les jugades.
  • El jugador escollirà el símbol que vol (X o O) i es farà un sorteig de qui comença la partida
  • L'ordinador analitzarà la situació del tauler per cercar la millor jugada a fer.
  • La partida finalitzarà en el moment que un dels jugadors aconsegueixi fer 3 fitxes en linia o quan el tauler estigui omplert.
  • Cal informar del resultat de la partida: Guanya la persona, l'oridnador o hi ha hagut un empat.
  • El programa permetrà tornar a jugar si així o vol el jugador.


Recursivitat

Obtingut de «http://wikiserver.infomerce.es/index.php?title=ASIX-M3-UF2-Banc_de_Solucions&oldid=15406»